Consider two lines L1 and L2 given by x-y=0 and x+y=0, respectively, and a moving point P(x,y). Let d(P,Li), i=1,2, represents the distance of point P from the line Li. If point P moves in a certain region R is such a way that 2≤d(P,L1)+d(P,L2)≤4,
find the area of region R. Solution in Bengali
Step by step video solution for Consider two lines L_(1) " and " L_(2) given by x-y=0 and x+y=0, respectively, and a moving point P(x,y). Let d(P,L_(i)), i=1,2, represents the distance of point P from the line L_(i). If point P moves in a certain region R is such a way that 2 le d(P,L_(1))+d(P,L_(2))le 4, find the area of region R. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Find the sum of the following series to n terms 5+7+13+31+85+
11:28View SolutionIn ABC,= if (a+b+c)(a−b+c)=3ac, then find ∠B.
11:03View SolutionConsider two lines L1andL2 given by x−y=0 and x+y=0 , respectively, and a moving point P(x,y). Let d(P,L1),i=1,2, represents the distance of point P from the line Lt If point P moves in a certain region R in such a way that 2≤d(P,P1)+d(P,L1)≤4 , find the area of region R.
View Solutiontheta_(1) and theta_(2) are the inclination of lines L_(1) and L_(2) with the x axis.If L_(1) and L_(2) pass through P(x,y) ,then the equation of one of the angle bisector of these lines is
View SolutionConsider a plane P≡2x+y−z≡0 a line x−32=y+1−3=z−2−1 and a point A(3,−4,1). L2 is a line passing through A intersecting L1 an parallel to the plane P
Plane containing L1 and L2 isView SolutionTwo straight lines l1 and l2 cross each other ar point P The line l1 is moving at a speed v1 perpendicular to itself & line l2 is moving at a speed v2 in the similar fashion. The speed of point P is :
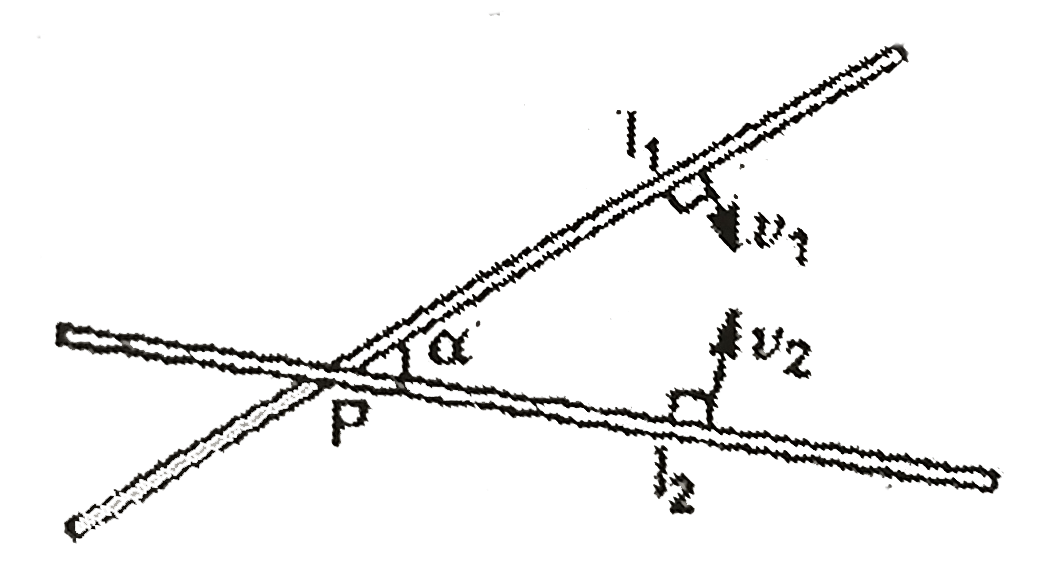 00:52View Solution
00:52View SolutionLet l1andl2 be the two skew lines. If P, Q are two distinct points on l1 and R, S are two distinct points on l2, then prove that PR cannot be parallel to QS.
View SolutionIf lines l1,l2 and l3 pass through a point P, then they are called…………. Lines.
View SolutionConsider the following lines :
L1:x−y−1=0
L2:x+y−5=0
L3:y−4=0
Let L1 is axis to a parabola, L2 is tangent at the vertex to this parabola and L3 is another tangent to this parabola at some point P.
Let 'C' be the circle circumscribing the triangle formed by tangent and normal at point P and axis of parabola. The tangent and normals at normals at the extremities of latus rectum of this parabola forms a quadrilateral ABCD.
Q. The equation of the circle 'C' is :06:59View SolutionConsider the following lines :
L1:x−y−1=0
L2:x+y−5=0
L3:y−4=0
Let L1 is axis to a parabola, L2 is tangent at the vertex to this parabola and L3 is another tangent to this parabola at some point P.
Let 'C' be the circle circumscribing the triangle formed by tangent and normal at point P and axis of parabola. The tangent and normals at normals at the extremities of latus rectum of this parabola forms a quadrilateral ABCD.
Q. The area of the quarilateral ABCD is :06:49View Solutionतीन समतल लीजिए
P1:x−y+z=1
P2:x+y−z=−1
P3:x−3y+3z=2
माना L1,L2,L3 क्रमशः समतल P2 व P3,P3 व P1 तथा P1 व P2 की प्रतिच्छेदी रेखायें हैं।
कथन-1: L1,L2 और L3 में से कम से कम दो रेखायें असमान्तर हैं।
क्योंकि कथन - 2 : तीनों समतलों का कोई सर्वनिष्ठ बिन्दु नहीं है।04:25View SolutionConsider, L_(1) : 2x + 3y + p – 3 = 0 , L_(2) : 2x + 3y + p + 3 = 0 , where p is a real number, and C : x^(2)+y^(2)+6x–10y+30=0 Statement-I : If line L_(1) is a chord of circle C, then line L_(2) is not always a diameter of circle C. and Statement-II : If line L_(1) is a diameter of circle C, then line L_(2) is not a chord of circle C.
View SolutionLet P represent the point (3, 6) on the parabola y2=12x. For the parabola y2=12x, if l1 is the length of the normal chord drawn at P and l2 is the length of the focal chord drawn through P, then l1l2=
View SolutionConsider the following lines :
L1:x−y−1=0
L2:x+y−5=0
L3:y−4=0
Let L1 is axis to a parabola, L2 is tangent at the vertex to this parabola and L3 is another tangent to this parabola at some point P.
Let 'C' be the circle circumscribing the triangle formed by tangent and normal at point P and axis of parabola. The tangent and normals at normals at the extremities of latus rectum of this parabola forms a quadrilateral ABCD.
Q. The equation of the circle 'C' is :03:15View SolutionConsider the following lines :
L1:x−y−1=0
L2:x+y−5=0
L3:y−4=0
Let L1 is axis to a parabola, L2 is tangent at the vertex to this parabola and L3 is another tangent to this parabola at some point P.
Let 'C' be the circle circumscribing the triangle formed by tangent and normal at point P and axis of parabola. The tangent and normals at normals at the extremities of latus rectum of this parabola forms a quadrilateral ABCD.
Q. The area of the quarilateral ABCD is :07:23View SolutionThe distance between two points P and Q is d and the lengths of projections of PQ on the coordinate planes are l1,l2,l3 then l1+l22+l23d2
04:52View Solution

