θ1andθ2 are the inclination of lines L1andL2 with the x-axis. If L1andL2 pass through P(x,y), then the equation of one of the angle bisector of these lines is
Step by step video & image solution for theta_1 and theta_2 are the inclination of lines L_1 and L_2 with the x-axis. If L_1 and L_2 pass through P(x,y), then the equation of one of the angle bisector of these lines is by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
θ1andθ2 are the inclination of lines L1andL2 with the x-axis. If L1andL2 pass through P(x1,y1), then the equation of one of the angle bisector of these lines is
View Solutionθ1 and θ2 are the inclination of lines L1andL2 with the x-axis. If L1andL2 pass through P(x1,y1) , then the equation of one of the angle bisector of these lines is (a) x−x1cos(θ1−θ22)=y−y1sin(θ1−θ22) (b)x−x1−sin(θ1−θ22)=y−y1cos(θ1−θ22) (c)x−x1sin(θ1−θ22)=y−y1cos(θ1−θ22) (d)x−x1−sin(θ1−θ22)=y−y1cos(θ1−θ22)
View Solution
Knowledge Check
The area of triangle formed by the lines l1andl2 and the x-axis is:
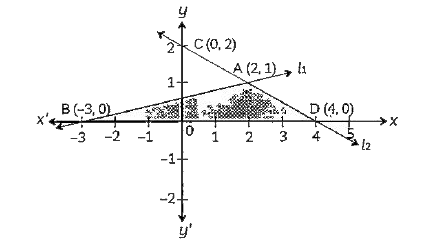 A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. units
A7 sq. unitsB92 sq.unitsC72 sq.unitsD4 sq. unitsA line L passeds through the points (1,1)and(2,0) and another line L' passes through (12,0) and perpendicular to L. Then the area of the triangle formed by the lines L, L' and Y-axis is
A158B254C258D2516
θ1 and θ2 are the inclination of lines L1andL2 with the x-axis. If L1andL2 pass through P(x1,y1) , then the equation of one of the angle bisector of these lines is
(a) x−x1cos(θ1−θ22)=y−y1sin(θ1−θ22) (b)x−x1−sin(θ1−θ22)=y−y1cos(θ1−θ22) (c)x−x1sin(θ1−θ22)=y−y1cos(θ1−θ22) (d)x−x1−sin(θ1+θ22)=y−y1cos(θ1+θ22)
View SolutionThe equations of bisectors of two lines L1&L2 are 2x−16y−5=0 and 64x+8y+35=0. lf the line L1 passes through (−11,4), the equation of acute angle bisector of L1 & L2 is:
View SolutionThe equations of bisectors of two lines L1&L2 are 2x−16y−5=0 and 64x+8y+35=0. lf the line L1 passes through (−11,4), the equation of acute angle bisector of L1 & L2 is:
View SolutionGiven equation of line L1 is y=4
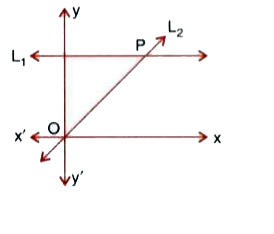
Write the slope of line L1 if L2 is the bisector of angle O.
View SolutionThe bisector of two lines L and L are given by 3x2−8xy−3y2+10x+20y−25=0. If the line L1 passes through origin, find the equation of line L2.
View SolutionIf lines l1,l2 and l3 pass through a point P, then they are called…………. Lines.
View Solution
