The lines y=m1x,y=m2xandy=m3x make equal intercepts on the line x+y=1. Then (a) 2(1+m1)(1+m3)=(1+m2)(2+m1+m3) (b)(1+m1)(1+m3)=(1+m2)(1+m1+m3) (c)(1+m1)(1+m2)=(1+m3)(2+m1+m3) (d)2(1+m1)(1+m3)=(1+m2)(1+m1+m3)Solution in Bengali
Step by step video & image solution for The lines y=m_1x ,y=m_2xa n dy=m_3x make equal intercepts on the line x+y=1. Then (a) 2(1+m_1)(1+m_3)=(1+m_2)(2+m_1+m_3) (b)(1+m_1)(1+m_3)=(1+m_2)(1+m_1+m_3) (c)(1+m_1)(1+m_2)=(1+m_3)(2+m_1+m_3) (d)2(1+m_1)(1+m_3)=(1+m_2)(1+m_1+m_3) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Find the sum of the following series to n terms 5+7+13+31+85+
03:45View SolutionIn ABC,= if (a+b+c)(a−b+c)=3ac, then find ∠B.
07:03View SolutionIf l_1^2+m_1^2+n_1^2=1 etc., and l_1 l_2+m_1 m_2+n_1 n_2 = 0, etc. and Delta=|(l_1,m_1,n_1),(l_2,m_2,n_2),(l_3,m_3,n_3)| then
01:22View SolutionProve that a point can be found which is at the same distance from each of the four points :(a m_1, a/(m_1))*(a m_2, a/(m_2))*(a m_3, a/(m_3))"and"(a/(m_1m_2 m_3), a m_1m_2m_3)
03:32View SolutionIf the lines whose equations are y=m1x+c1,y=m2x+c2andy=m3x+c3 meet in a point, then prove that : m1(c2−c3)+m2(c3−c1)+m3(c1−c2)=0
03:42View SolutionIf (mi,1mi) , i = 1, 2, 3, 4 are concyclic points, then the value of m1m2m3m4 is :
05:09View Solutionm1,m2 व m3 द्रव्यमान के तीन पिण्ड क्रमागत द्रव्यमान रहित डोरी से जुड़े हैं और एक घर्षण रहित मेज पर रखे हैं | यदि m3 द्रव्यमान को बल F से खींचा जाए, तो m2 व m3 द्रव्यमानों के बीच डोरी में तनाव होगा :
04:10View Solutionयहाँ दर्शाये गये निकाय में तीन पिंड m1,m2 और m3 एक रस्सी से जुड़े है जो एक घिरनी के ऊपर से होकर गुजरती है। m1 मुक्त रूप से लटका है औरm2 तथा m3 एक रुक्ष क्षैतिज मेज पर है, जिसका घर्षण गुणांक =μ है। घिरनी घर्षणरहित है और इसका द्रव्यमान नगण्य है। यदि m1=m2=m3=m है, तो m1 का अधोमुखी (नीचे की ओर) त्वरण होगा:
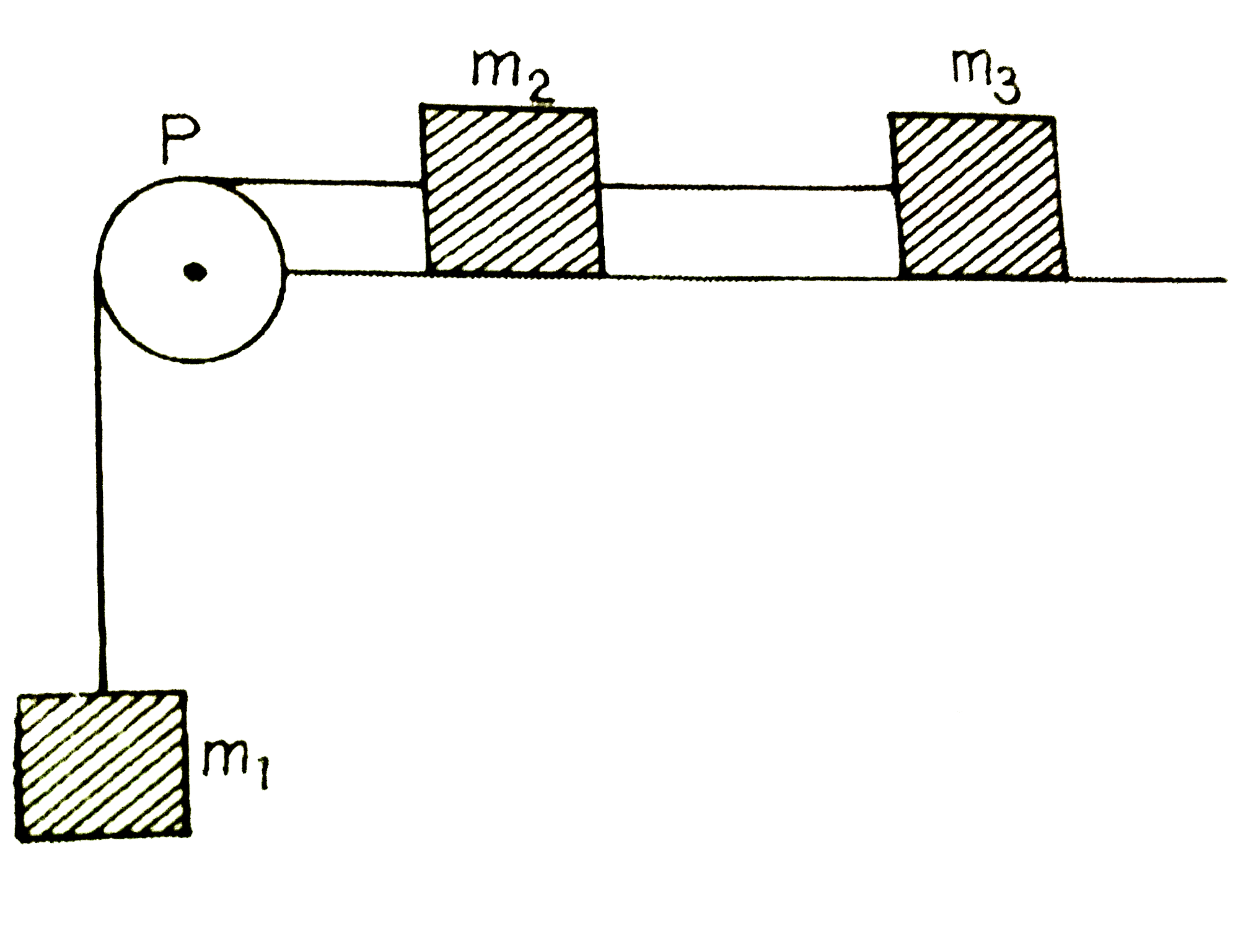 04:32View Solution
04:32View SolutionIf l21+m21+n21=1 etc., and l1l2+m1m2+n1n2=0, etc. and Δ=∣∣ ∣∣l1m1n1l2m2n2l3m3n3∣∣ ∣∣ then
View SolutionThe lines y=m1x,y=m2xandy=m3x make equal intercepts on the line x+y=1. Then (a) 2(1+m1)(1+m3)=(1+m2)(2+m1+m3) (b)(1+m1)(1+m3)=(1+m2)(1+m1+m3) (c)(1+m1)(1+m2)=(1+m3)(2+m1+m3) (d)2(1+m1)(1+m3)=(1+m2)(1+m1+m3)
05:03View SolutionGravitational force between masses m_1 and m_2 is F. If a third mass m_3 is placed near m_2 and m_3 then the force between m_1 and m_2 would be
05:30View SolutionIf three lines whose equations are y =m_1 x+c_1, y=m_2 x+c_2 and y=m_3 x+c_3 are concurrent, then show that m_1(c_2-c_3)+m_2(c_3-c_1)+m_3(c_1-c_2)=0
07:02View SolutionIf the lines whose equations are y=m1x+c1,y=m2x+c2andy=m3x+c3 meet in a point, then prove that : m1(c2−c3)+m2(c3−c1)+m3(c1−c2)=0
06:48View SolutionProve that a point can be found which is at the same distance from each of the four points :(am1,am1),(am2,am2),(am3,am3)and(am1m2m3,am1m2m3)
04:11View SolutionShow that the lines y−m1x−c1=0, y−m2x−c2=0and y−m3x−c3=0 form an isosceles triangle with the first line as base if : (1+m1m2)(m1−m3)+(1+m1m3)(m1−m2)=0
06:47View SolutionIf l_1^2+m_1^2+n_1^2=1 etc., and l_1 l_2+m_1 m_2+n_1 n_2 = 0 , etc. and Delta=|(l_1,m_1,n_1),(l_2,m_2,n_2),(l_3,m_3,n_3)| then
05:09View Solution

