Let C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point .
List 1
a) P
lies inside
C1
but outside
C2
b)P
lies inside
C2
but outside
C1
c)P
lies outside
C1
but outside
C2
d)P
does not lie inside
C2
List 2
p)λ ϵ (−∞,−1)∪(0,∞)
q)λ ϵ (−∞,−1)∪(1,∞)
r)λ ϵ (−1,0)
s)λ ϵ (0,1)
Solution in Bengali
Step by step video & image solution for Let C_1 and C_2 be two circles whose equations are x^2+y^2-2x=0 and x^2+y^2+2x=0 and P(lambda, lambda) is a variable point . List 1 a) P lies inside C_1 but outside C_2 b)P lies inside C_2 but outside C_1 c)P lies outside C_1 but outside C_2 d)P does not lie inside C_2 List 2 p)λ ϵ (−∞,−1)∪(0,∞) q)λ ϵ (−∞,−1)∪(1,∞) r)λ ϵ (−1,0) s)λ ϵ (0,1) by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
877 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
The equation esinx−e−sinx−4=0 has
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to
View SolutionLet C_1 and C_2 be parabolas x^2 = y - 1 and y^2 = x-1 respectively. Let P be any point on C_1 and Q be any point C_2. Let P_1 and Q_1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P_1 lies on C_2 and Q_1 lies on C_1 and PQ >= [P P_1, Q Q_1]. Hence or otherwise , determine points P_0 and Q_0 on the parabolas C_1 and C_2 respectively such that P_0 Q_0 <= PQ for all pairs of points (P,Q) with P on C_1 and Q on C_2
View SolutionConsider circles C_1 : x^2 +y^2 + 2x-2y + p = 0, C_2 : x^2+y^2-2x+2y-p=0 and C_3 : x^2+y^2=p^2 Statement I: If the circle C_3 intersects C_1, orthogonally then C_2 does not represent a circle Statement II: If the circle C_3, intersects C_2 orthogonally then C_2 and C_3 have equal radii. Then which of the following statements is true ?
View Solution∣∣ ∣ ∣∣111nc1n+1c1n+2c1n+1c2n+2c2n+3c2∣∣ ∣ ∣∣=1
View SolutionConsider the curves C1:y2andC2:x2+y2−6x+1=0
Assertion (A) The common tangents to the curves C1andC2 are othogonal.
Reason ( R ) x-y+1=0 and x+y+1=0 are the common tangents to the curves C1andC2 The correct answer is
View SolutionLet C1and C2 be two circles with C2 lying inside C1 A circle C lying inside C1 touches C1 internally and C2 externally. Identify the locus of the centre of C
View SolutionTwo circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
View SolutionLet C1 and C2 be two circles whose equations are x2+y2−2x=0 and x2+y2+2x=0 and P(λ,λ) is a variable point . List 1 a) P lies inside C1 but outside C2 2)P lies inside C2 but outside C1 c)P lies outside C1 but outside C2 d)P does not lie inside C2 List 2 p)λ ϵ (−∞,−1)∪(0,∞) q)λ ϵ (−∞,−1)∪(1,∞) r)λ ϵ (−1,0) s)λ ϵ (0,1)
View SolutionConsider three circles C1,C2andC3 such that C2 is the director circle of C1,andC3 is the director circle of C2. Tangents to C1, from any point on C3 intersect C2, at PandQ. Find the angle between the tangents to C2 at P and Q. Also identify the locus of the point of intersec- tion of tangents at PandQ.
View SolutionThe value of ∣∣111nCn+21Cn+41Cn1Cn+22Cn+42C2∣∣ is
View Solutionदिखाए गये चित्रानुसार दोनो वृतों के केंद्रों C1 तथा C2 के मध्य दुरी 35 है अर्थात C1C2=35 तथा C1 व C2 केंद्रों वाले वृतों की त्रिज्याएँ क्रमशः 12 व 9 है । यदि वृतों की उभयनिष्ठ आंतरिक स्पर्श रेखा तथा C1C2 का प्रतिच्छेद बिंदु P है, तो l(C1P) का मान होगा
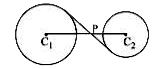
(i) 18 (ii) 20 (iii) 12 (iv) 15
View SolutionThe equation of a circle C1 is x2+y2−4x−2y−11=0 A circleC2 of radius 1 rolls on the outside of the circle C1 The locus of the centre C2 has the equation
View SolutionLet C1 and C2 be parabolas x2=y−1 and y2=x−1 respectively. Let P be any point on C1 and Q be any point C2. Let P1 and Q1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P1 lies on C2 and Q1 lies on C1 and PQ≥[PP1,QQ1]. Hence or otherwise , determine points P0 and Q0 on the parabolas C1 and C2 respectively such that P0Q0≤PQ for all pairs of points (P,Q) with P on C1 and Q on C2
View SolutionLet C_1 and C_2 be parabolas x^2 = y - 1 and y^2 = x-1 respectively. Let P be any point on C_1 and Q be any point C_2 . Let P_1 and Q_1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P_1 lies on C_2 and Q_1 lies on C_1 and PQ >= [P P_1, Q Q_1] . Hence or otherwise , determine points P_0 and Q_0 on the parabolas C_1 and C_2 respectively such that P_0 Q_0 <= PQ for all pairs of points (P,Q) with P on C_1 and Q on C_2
View SolutionLet C_1 and C_2 be two circles whose equations are x^2+y^2-2x=0 and x^2+y^2+2x=0 and P(lambda, lambda) is a variable point
View Solution
