Two circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZSolution in Bengali
Step by step video & image solution for Two circles C_1 and C_2 intersect at two distinct points PandQ in a line passing through P meets circles C_1andC_2 at AandB , respectively. Let Y be the midpoint of A B and Q Y meets circles C_1 andC_2 at Xa n dZ respectively. Then prove that Y is the midpoint of X Z by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
877 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
The equation esinx−e−sinx−4=0 has
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to
View SolutionLet C_1 and C_2 be parabolas x^2 = y - 1 and y^2 = x-1 respectively. Let P be any point on C_1 and Q be any point C_2. Let P_1 and Q_1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P_1 lies on C_2 and Q_1 lies on C_1 and PQ >= [P P_1, Q Q_1]. Hence or otherwise , determine points P_0 and Q_0 on the parabolas C_1 and C_2 respectively such that P_0 Q_0 <= PQ for all pairs of points (P,Q) with P on C_1 and Q on C_2
View SolutionIf the lines whose equations are y=m1x+c1,y=m2x+c2andy=m3x+c3 meet in a point, then prove that : m1(c2−c3)+m2(c3−c1)+m3(c1−c2)=0
View SolutionC1:x2+y2=a2 and C2:x2+y2=b2 are two contentric circles. A line through the centre of these circles intersects them at P and respectively. If the lines through P and Q parallel to y-axis and x-axis respectively meet at the point R, then the locus of R is
View SolutionTwo circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
View SolutionConsider three circles C1,C2andC3 such that C2 is the director circle of C1,andC3 is the director circle of C2. Tangents to C1, from any point on C3 intersect C2, at PandQ. Find the angle between the tangents to C2 at P and Q. Also identify the locus of the point of intersec- tion of tangents at PandQ.
View Solutionबिन्दु P(6,5) से परवलय y2=4x पर डाली गयी स्पर्श रेखाएँ परवलय को Qऔर R पर स्पर्श करती है। यदि वृत्त C1 परवलय को Q पर स्पर्श करता है तथा वृत्त C2 परवलय R पर स्पर्श करता है तथा दोनों वृत्त C1 और C2 परवलय । की नाभि से होकर जाते है। तब
वृत्त C2 की त्रिज्या है
View Solutionदिखाए गये चित्रानुसार दोनो वृतों के केंद्रों C1 तथा C2 के मध्य दुरी 35 है अर्थात C1C2=35 तथा C1 व C2 केंद्रों वाले वृतों की त्रिज्याएँ क्रमशः 12 व 9 है । यदि वृतों की उभयनिष्ठ आंतरिक स्पर्श रेखा तथा C1C2 का प्रतिच्छेद बिंदु P है, तो l(C1P) का मान होगा
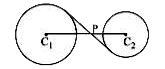
(i) 18 (ii) 20 (iii) 12 (iv) 15
View Solutionx2+y2=4 এবং (x−2)2+y2=1 বৃত্তদ্বয়ের কেন্দ্রবিন্দুটি যথাক্রমে C1 এবং C2 । P এবং Q বৃত্তদ্বয়ের ছেদবিন্দুদ্বয় হলে C1PQ এবং C2PQ ত্রিভুজদ্বয়ের ক্ষেত্রফলের অনুপাত হবে
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 and C1 Q are in
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 are C1 Q are in
View SolutionIf the lines whose equations are y=m1x+c1,y=m2x+c2andy=m3x+c3 meet in a point, then prove that : m1(c2−c3)+m2(c3−c1)+m3(c1−c2)=0
View SolutionLet C1 and C2 be parabolas x2=y−1 and y2=x−1 respectively. Let P be any point on C1 and Q be any point C2. Let P1 and Q1 be the reflection of P and Q, respectively w.r.t the line y = x then prove that P1 lies on C2 and Q1 lies on C1 and PQ≥[PP1,QQ1]. Hence or otherwise , determine points P0 and Q0 on the parabolas C1 and C2 respectively such that P0Q0≤PQ for all pairs of points (P,Q) with P on C1 and Q on C2
View SolutionEvaluate |^x C_1^x C_2^x C_3^y C_1^y C_2^y C_3^z C_1^z C_2^z C_3|
View Solution
