TP and TQ are tangents to the parabola, y2=4ax at P and Q. If the chord PQ passes through the fixed point (-a,b), then find find the locus of T.Solution in Bengali
Step by step video & image solution for TP and TQ are tangents to the parabola, y^(2)=4ax at P and Q. If the chord PQ passes through the fixed point (-a,b), then find find the locus of T. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - All Questions
877 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE PUBLICATIONCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Multiple correct answers type
11 Videos
Similar Questions
The equation esinx−e−sinx−4=0 has
View SolutionLet →a=a1ˆi+a2ˆj+a3ˆk,→b=b1ˆi+b2ˆj+b3ˆk and →c=c1ˆi+c2ˆj+c3ˆk be three non- zero vectors such that →c is a unit vectors perpendicular to both the vectors →a and →b. If the angle between →a and →b is π6 then
∣∣ ∣∣a1a2a3b1b2b3c1c2c3∣∣ ∣∣2 is equal to
View SolutionTP and TQ are tangents to the parabola y2=4ax at PandQ, respectively. If the chord PQ passes through the fixed point (−a,b), then find the locus of T.
View SolutionLet y^(2)=4ax be a parabola and PQ be a focal chord of parabola.Let T be the point of intersection of tangents at P and Q. Then
View SolutionTP&TQ are tangents to the parabola,y^(2)=4ax at P and Q. If the chord passes through the point (-a,b) then the locus of T is
View SolutionTP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q'. Prove that (TP')/(TP)+(TQ')/(TQ)=1
View SolutionFind the locus of point whose chord of contact w.r.t. to the parabola y2=4bx is the tangent of the parabola y2=4ax.
View SolutionFind the locus of middle of the chord of the parabola y^(2) = 4ax which pass through a given (p, q).
View SolutionThe locus of middle points of normal chords of the parabola y2=4ax is
View SolutionA variable tangent to the parabola y2=4ax meets the parabola y2 +4ax=0 at the points P,Q . The locus of the middle point of PQ is
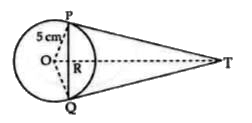
View SolutionIn the figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at T. Find TP and TQ.
View SolutionTP and TQ are tangents to the parabola y2=4ax at PandQ, respectively. If the chord PQ passes through the fixed point (−a,b), then find the locus of T.
View SolutionTP and TQ are tangents to the parabola y2=4ax at PandQ, respectively. If the chord PQ passes through the fixed point (−a,b), then find the locus of T.
View Solutionपरवलय y2=4ax के बिन्दु P व Q पर TP और TQ स्पर्श रेखाएं है। यदि जीवा PQ एक स्थिर बिन्दु (−a,b) से गुजरती है, तो T का बिन्दु पथ है-
View SolutionTP and TQ are any two tangents to a parabola and the tangent at a third point R cuts them in P' and Q'. Prove that TP'TP+TQ'TQ=1
View SolutionTP and TQ are tangents to the parabola y2=4ax at PandQ, respectively. If the chord PQ passes through the fixed point (−a,b), then find the locus of T.
View Solution
