[Bengali] Let two non-collinear unit vector hat a a n d hat b form

If sec x + tan x =22/7 , find the value of tanx/2

$\to a = 2 \to i + \to j + \to k$ , $\to b = b_{1} ˆ i + b_{2} ˆ j + b_{3} ˆ k$ ,
$\to a \times \to b = 5 ˆ i + 2 ˆ j - 12 ˆ k, \to a . \to b = 11$ , then $b_{1} + b_{2} + b_{3} =$

View Solution

The position vectors of the points $P a n d Q$ with respect to the origin $O$ are $\to a = ˆ i + 3 ˆ j - 2 ˆ k$ and $\to b = 3 ˆ i - ˆ j - 2 ˆ k,$ respectively. If $M$ is a point on $P Q,$ such that $O M$ is the bisector of $∠ P O Q,$ then $\to O M$ is a. $2 (ˆ i - ˆ j + ˆ k)$ b. $2 ˆ i + ˆ j - 2 ˆ k$ c. $2 (- ˆ i + ˆ j - ˆ k)$ d. $2 (ˆ i + ˆ j + ˆ k)$

View Solution

Let two non-collinear unit vector $ˆ a$ a n d $ˆ b$ form an acute angle. A point $P$ moves so that at any time $t,$ the position vector $O P (w h e r e O$ is the origin $)$ is given by $ˆ a cos t + ˆ b sin t . W h e n P$ is farthest from origin $O,$ let $M$ be the length of $O P a n d ˆ u$ be the unit vector along $O P .$ Then (a) $ˆ u = \frac{ˆ a + ˆ b}{∣ ∣ ˆ a + ˆ b ∣ ∣} a n d M = {(1 + ˆ a . ˆ b)}^{1 / 2}$ (b) $ˆ u = \frac{ˆ a - ˆ b}{∣ ∣ ˆ a - ˆ b ∣ ∣} a n d M = {(1 + ˆ a .^)}^{1 / 2}$ (c) $ˆ u = \frac{ˆ a + ˆ b}{∣ ∣ ˆ a + ˆ b ∣ ∣} a n d M = {(1 + 2 ˆ a . ˆ b)}^{1 / 2}$ (d) $ˆ u = \frac{ˆ a - ˆ b}{∣ ∣ ˆ a - ˆ b ∣ ∣} a n d M = {(1 + 2 ˆ a . ˆ b)}^{1 / 2}$

View Solution

Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and hat(i), hat(j), hat(k) are unit vectors)

View Solution

माना दो असंरेखीय इकाई दिशा $ˆ a$ और $ˆ b$ एक न्यूनकोण बनाते हैं एक बिंदु P इस प्रकार गतिमान है कि किसी समय t पर स्थिति सदिश $- - \to O P$ (जहां O मूल बिंदु है) $ˆ a cos t + ˆ b sin t$ द्वारा दिया जाता है। माना जब P मूल बिंदु O से अधिकतम दूरी पर है एवं $- - \to O P$ की लम्बाई M तथा $ˆ u, - - \to O P$ के अनुदिश इकाई सदिश हे तब

View Solution

The position vectors of the vertices $A, B, a n d C$ of a triangle are $ˆ i + ˆ j, ˆ j + ˆ k a n d ˆ i + ˆ k$ , respectively. Find the unite vector $ˆ r$ lying in the plane of $A B C$ and perpendicular to $I A, w h e r e I$ is the incentre of the triangle.

View Solution

The position vectors of the points $P a n d Q$ with respect to the origin $O$ are $\to a = ˆ i + 3 ˆ j - 2 ˆ k$ and $\to b = 3 ˆ i - ˆ j - 2 ˆ k,$ respectively. If $M$ is a point on $P Q,$ such that $O M$ is the bisector of $∠ P O Q,$ then $\to O M$ is a. $2 (ˆ i - ˆ j + ˆ k)$ b. $2 ˆ i + ˆ j - 2 ˆ k$ c. $2 (- ˆ i + ˆ j - ˆ k)$ d. $2 (ˆ i + ˆ j + ˆ k)$

View Solution

The position vectors of points $A a n d B$ w.r.t. the origin are $\to a = ˆ i + 3 ˆ j - 2 ˆ k$ , $\to b = 3 ˆ i + ˆ j - 2 ˆ k$ respectively. Determine vector $\to O P$ which bisects angle $A O B,$ where $P$ is a point on $A B .$

View Solution

Given unit vectors $ˆ m, ˆ n a n d ˆ p$ such that angel between $ˆ m a n d ˆ n$ is $α$ and angle between $ˆ p a n d (ˆ m \times ˆ n)$ is also $α, t h e n [ˆ n ˆ p ˆ m] =$

View Solution

The angles of triangle, two of whose sides are represented by vectors $\sqrt{3} (\to a \times \to b) a n d \to b - (ˆ a . \to b) ˆ a, w h e r e \to b$ is a non zero vector and $ˆ a$ is unit vector in the direction of $\to a,$ are

View Solution

Let two non-collinear unit vector $ˆ a$ a n d $ˆ b$ form an acute angle. A point $P$ moves so that at any time $t,$ the position vector $O P (w h e r e O$ is the origin $)$ is given by $ˆ a cos t + ˆ b sin t . W h e n P$ is farthest from origin $O,$ let $M$ be the length of $O P a n d ˆ u$ be the unit vector along $O P .$ Then (a) $ˆ u = \frac{ˆ a + ˆ b}{∣ ∣ ˆ a + ˆ b ∣ ∣} a n d M = {(1 + ˆ a . ˆ b)}^{1 / 2}$ (b) $ˆ u = \frac{ˆ a - ˆ b}{∣ ∣ ˆ a - ˆ b ∣ ∣} a n d M = {(1 + ˆ a .^)}^{1 / 2}$ (c) $ˆ u = \frac{ˆ a + ˆ b}{∣ ∣ ˆ a + ˆ b ∣ ∣} a n d M = {(1 + 2 ˆ a . ˆ b)}^{1 / 2}$ (d) $ˆ u = \frac{ˆ a - ˆ b}{∣ ∣ ˆ a - ˆ b ∣ ∣} a n d M = {(1 + 2 ˆ a . ˆ b)}^{1 / 2}$

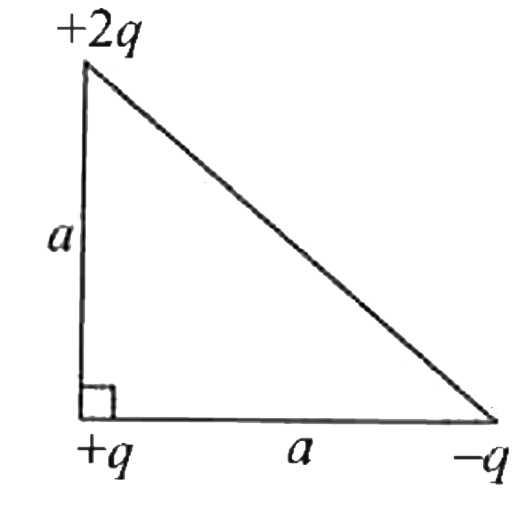
View Solution

Three charges $+ q, - q, and + 2 q$ are placed at the verticles of a right angled triangle (isoceles triangle) as shown. The net electrostatic energy of the configuration is :
ocr_image

View Solution

The position vectors of the vertices $A, B, a n d C$ of a triangle are $ˆ i + ˆ j, ˆ j + ˆ k a n d ˆ i + ˆ k$ , respectively. Find the unite vector $ˆ r$ lying in the plane of $A B C$ and perpendicular to $I A, w h e r e I$ is the incentre of the triangle.

View Solution

The position vectors of the points $P a n d Q$ with respect to the origin $O$ are $\to a = ˆ i + 3 ˆ j - 2 ˆ k$ and $\to b = 3 ˆ i - ˆ j - 2 ˆ k,$ respectively. If $M$ is a point on $P Q,$ such that $O M$ is the bisector of $∠ P O Q,$ then $\to O M$ is a. $2 (ˆ i - ˆ j + ˆ k)$ b. $2 ˆ i + ˆ j - 2 ˆ k$ c. $2 (- ˆ i + ˆ j - ˆ k)$ d. $2 (ˆ i + ˆ j + ˆ k)$

View Solution

The position vectors of points $A a n d B$ w.r.t. the origin are $\to a = ˆ i + 3 ˆ j - 2 ˆ k$ , $\to b = 3 ˆ i + ˆ j - 2 ˆ k$ respectively. Determine vector $\to O P$ which bisects angle $A O B,$ where $P$ is a point on $A B .$

View Solution

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-VECTOR ALGEBRA-All Questions