Statement 1 : Points A(1,0),B(2,3),C(5,3),andD(6,0) are concyclic. Statement 2 : Points A,B,C,andD form an isosceles trapezium or ABandCD meet at E. Then EA⋅EB=EC⋅ED.Solution in Bengali
Step by step video & image solution for Statement 1 : Points A(1,0),B(2,3),C(5,3),a n dD(6,0) are concyclic. Statement 2 : Points A , B , C ,a n dD form an isosceles trapezium or A Ba n dC D meet at Edot Then E A*E B=E C*E Ddot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type
6 Videos
- VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSBOOK - CENGAGE PUBLICATIONCHAPTER - VECTORS TRIPLE PRODUCTS, RECIPROCAL SYSTEM OF VECTORSEXERCISE - DPP 2.4
20 Videos
Similar Questions
If sec x + tan x =22/7 , find the value of tanx/2
View Solution→a=2→i+→j+→k, →b=b1ˆi+b2ˆj+b3ˆk,
→a×→b=5ˆi+2ˆj−12ˆk,→a.→b=11, then b1+b2+b3=
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionStatement 1 : Points A(1,0),B(2,3),C(5,3),andD(6,0) are concyclic. Statement 2 : Points A,B,C,andD form an isosceles trapezium or ABandCD meet at E. Then EA.EB=EC.ED.
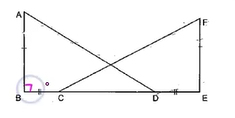
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: ar(EFC)=12ar(EBF)
View SolutionStatement 1 : Points A(1,0),B(2,3),C(5,3),andD(6,0) are concyclic. Statement 2 : Points A,B,C,andD form an isosceles trapezium or ABandCD meet at E. Then EA.EB=EC.ED.
View SolutionFrom a point O inside a triangle ABC, perpendiculars OD,OEandOf are drawn to rthe sides BC,CAandAB, respecrtively. Prove that the perpendiculars from A,B,andC to the sides EF,FDandDE are concurrent.
View SolutionAD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC . Prove that AE=BD.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC~EDA.
View SolutionABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View SolutionIn Figure, it is given that AE=AD and BD=CE. Prove that AEB ≅ADC
View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
View SolutionIn Figure, AB⊥BE and FE ⊥BE. If BC=DE and AB=EF, then ABD is congruent to: EFC (b) ECF (c) CEF (d) FEC
View SolutionABCD is a parallelogram and E is the mid-point of BC, DE and AB when produced meet at F. Then AF=
View Solution
