Let l1andl2 be the two skew lines. If P,Q are two distinct points on l1ndR,S are two distinct points on l2, then prove that PR cannot be parallel to QS.Solution in Bengali
Step by step video & image solution for Let l_1a n dl_2 be the two skew lines. If P ,Q are two distinct points on l_1n dR , S are two distinct points on l_2, then prove that P R cannot be parallel to Q Sdot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
View SolutionIf the distance between the plane ax 2y + z = d and the plane containing the lines x−12=y−23=z−34 and x−23=y−34=z−45 is √6 , then value of |d| is
View SolutionProve that pxq−r+qxr−p+rxp−q>p+q+r,wherep,q,r are distinct andx≠1.
View SolutionProve that two distinct lines cannot have more that one point in common
View SolutionLet l1andl2 be the two skew lines. If P, Q are two distinct points on l1 and R, S are two distinct points on l2, then prove that PR cannot be parallel to QS.
View SolutionTwo circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
View SolutionLet l1andl2 be the two skew lines. If P,Q are two distinct points on l1ndR,S are two distinct points on l2, then prove that PR cannot be parallel to QS.
View SolutionLet l1andl2 be the two skew lines. If P, Q are two distinct points on l1 and R, S are two distinct points on l2, then prove that PR cannot be parallel to QS.
View SolutionIn Figure, common tangents P Q and RS to two circle intersect at A. Prove that PQ=RS
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionPQR is a triangle is which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT
View SolutionPQ and RS are two parallel chords of a circle and lines RP and SQ intersect each other at O as shown in Figure. Prove that OP=OQ
View SolutionLet P and Q be any two points. Find the coordinates of the point R which divides PQ externally in the ratio 2:1 and verify that Q is the mid point of PR .
View SolutionLet p,q,r be distinct positive numbers. Three lines px+qy+r=0,qx+ry+p=0 and rx+py+q=0 are concurrent, if
View SolutionIn the following diagram, lines l, m and n are parallel to each other. Two transversals p and q intersect the parallel lines at points A, B, C and P, Q, R as shown.
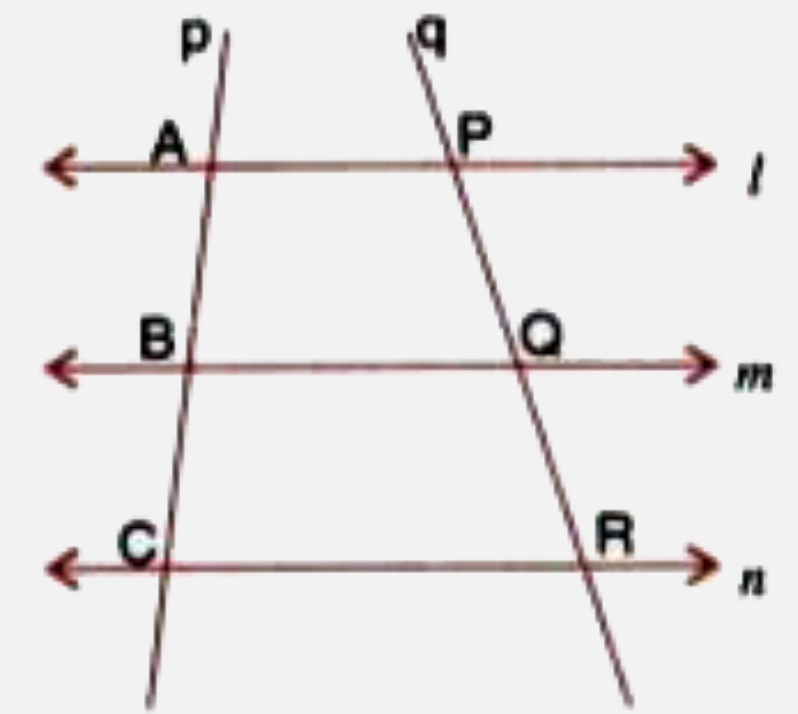
Prove that : ABBC=PQQR
Join A and R. Let AR meets BQ at point D.
View SolutionIf lines px+qy+r=0,qx+ry+p=0andrx+py+q=0 are concurrent, then prove that p+q+r=0(wherep,q,r are distinct).
View Solution
