n
whole are randomly chosen and multiplied
Column I,
Column II
The
probability that the last digit is 1,3,7, or 9 is, p. 8n−4n10n
The
probability that the last digit is 2,4,6, or 8 is, q. 5n−4n10n
The
probability that the last digit is 5 is, r. 4n10n
The
probability that the last digit is zero is, s. 10n−8n−5n+4n10nSolution in Bengali
abcdqssr
abcdrqqp
abcdqpps
abcdqspr
The correct Answer is:A, B, C, D
a. The required event will occur if last digit in all the chosen numbers is 1, 3, 7, or 9. Therefore, the required probability is (4/10)n.
b. The required probability is equal to the probability that the last digit is 2, 4, 6, 8 and is given by
P(last digit is 1, 2, 3, 4, 6, 7, 8, 9)
-P (last digit is 1, 3, 7, 9) = 8n−4n10n
c. P(1, 3, 5, 7, 9) - P(1, 3, 7, 9) = 5n−4n10n
d. The required probability is
P(0,5)−P(5)=(10n−8n)−(5n−4n)10n
P(0,5)−P(5)=(10n−8n)−(5n−4n)10n
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Numerical Value Type7videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - ARCHIVES4videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Comprehension14videos
PROBABILITY I
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions470videos
PROBABILITY
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE6videos
PROBABILITY II
Similar Questions
If the probability of a six digit number N whose six digit sare 1,2,3,4,5,6 written as random order is divisible by 6 is p, then the value of 1/p is__________.
04:03View SolutionFour numbers are chosen at random (without replacement) from the set {1, 2, 3, ....., 20}. Statement-1: The probability that the chosen numbers when arranged in some order will form an AP Is 185 . Statement-2: If the four chosen numbers form an AP, then the set of all possible values of common difference is {1, 2, 3, 4, 5}. (1) Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation for Statement-1 (2) Statement-1 is true, Statement-2 is false (3) Statement-1 is false, Statement-2 is true (4) Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation for Statement-1
View SolutionA shopping mall is running a scheme: Each packet of detergent SURF contains a coupon which bears letter of the word SURF, if a person buys at least four packets of detergent SURF, and produce all the letters of the word SURF, then he gets one free packet of detergent.
If a person buys 8 such packets, then the probability that he gets two free packets isView SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
05:05View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionMatch the intermediates given in Column I with their probable structure in Column II
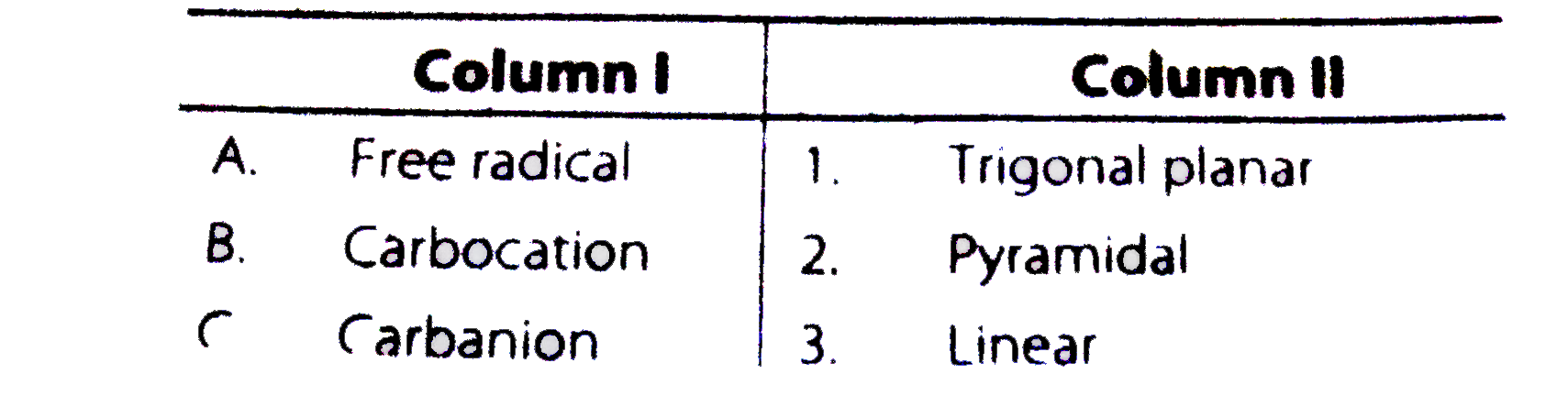 View Solution
View SolutionColumn I Column II
01:15View SolutionMatch the description in Column I with graph provided in Column II. For n moles of ideal gas at temperature 'T'. Column I Column II
04:47View SolutionTwo whole numbers are randomly chosen and multiplied, then the chance that their product is divisible by 5 is
03:55View SolutionColumn-I Column-II
04:37View SolutionColumn-I Column-II
02:36View Solutionవేర్ల ద్వారా శాఖీయోత్పత్తి జరిపే మొక్కbr i) డాలియాbr ii) ముల్లంగిbr iii) క్యారెట్br iv) క్యాబేజిbr
View Solutionकॉलम - I की सूची में दी गई भौतिक राशियों को कॉलम - II की सूची में यादृच्छिक रूप से दिए गए उनके मानों के साथ मिलाएँ।
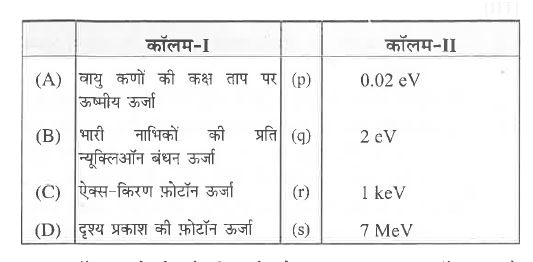 View Solution
View SolutionMatch the intermediates given in Column I with their probable structure in Column II
02:21View Solutionn whole are randomly chosen and multiplied
Column I, Column II
The probability that the last digit is 1,3,7, or 9 is, p. 8n−4n10n
The probability that the last digit is 2,4,6, or 8 is, q. 5n−4n10n
The probability that the last digit is 5 is, r. 4n10n
The probability that the last digit is zero is, s. 10n−8n−5n+4n10n03:02View SolutionColumn-I, Column-II
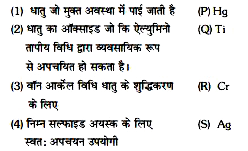 05:34View Solution
05:34View Solution

