Statement 1: There exist two points on the x−11=y−1=z+22 which are at a distance of 2 units from point (1,2,−4). Statement 2: Perpendicular distance of point (1,2,−4) form the line x−11=y−1=z+22 is 1 unit.Solution in Bengali
Both the statements are true, and Statement 2 is the correct explanation for Statement 1.
Both the Statements are true, but Statement 2 is not the correct explanation for Statement 1.
Statement 1 is true and Statement 2 is false.
Statement 1 is false and Statement 2 is true.
The correct Answer is:b
Any point on the line x−11=y−1=z+22 is
B(t+1,−t,2t−2),t∈R.
Also, AB is perpendicular to the line, where A is (1,2,−4). Thus,
1(t)−(−t−2)+2(2t+2)=0
or 6t+6=0
or t=−1
Point B is (0,1,−4)
Hence, AB=√1+1+0=√2
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - LINKED COMPREHENSION TYPE12videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE17videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
Given four points A(2,1,0),B(1,0,1),C(3,0,1)andD(0,0,2). Point D lies on a line L orthogonal to the plane determined by the points A, B and C.
The equation of the plane ABC is07:16View Solution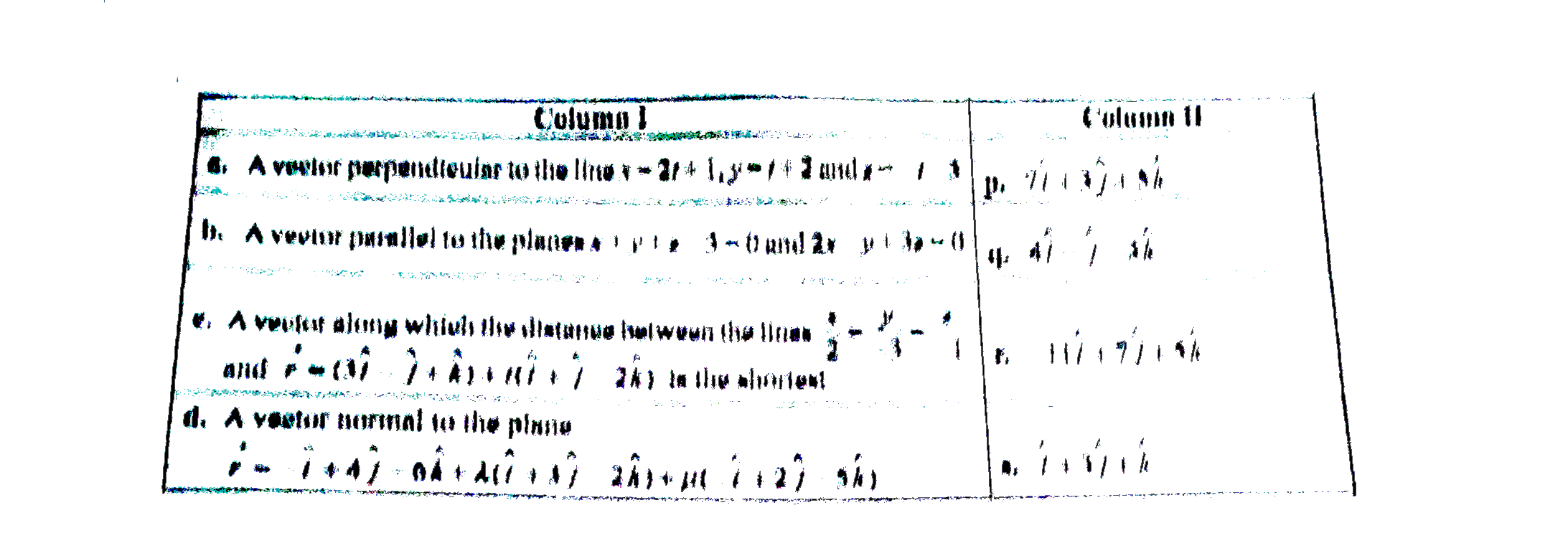
06:35View SolutionLet PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
11:11View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
06:37View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
03:34View SolutionStatement 1: There exist two points on the x−11=y−1=z+22 which are at a distance of 2 units from point (1,2,−4). Statement 2: Perpendicular distance of point (1,2,−4) form the line x−11=y−1=z+22 is 1 unit.
09:08View SolutionThe perpendicular distance of the point (1,2,3) from the line (x-1)/(2)=(y-3)/(1)=(z-4)/(1)
07:03View SolutionStatement 1: A point on the line x+23=y+12=z−32 at a distance 3√2 from the point (1,2,3) lies on the lne x+75=y+t4=z−21
Statement 2: If d is the distance between the point (−1,−5,−10) and the point of intersectionof the line x−23=y+14=z−212 with the plane x−y+z=5 then d=1303:55View SolutionStatement 1: The shortest distance between the lines x2=y−1=z2 and x−1−2=y−1−2=z−14 is √2. Statement 2: The shortest distance between two parallel lines is the perpendicular distance from any point on one of the lines to the other line.
04:45View SolutionShow that the distance of the point of intersection of the line (x-2)/3=(y+1)/4=(z-2)/12 and the plane (x-y+z=5) from the point (-1,-5,-10) is 13 units.
04:13View Solutionबिन्दु (1,2-3) से रेखा x−12=y−3−2=z1 पर लम्ब पाद ज्ञात कीजिए।
07:36View SolutionFind the perpendicular distance of the point (1,1,1) from the line x−22=y+32=z−1.
07:58View SolutionThe equation of line is x−12=y+1−2=z+11. The co-ordinates of the point on the line at a distance of 3 units from the point (1,−1,−1) is
07:50View Solutionसरल रेखा x+61=y−22=z+14 पर बिंदु (-6, 2, -1) से 3 दूरी पर एक बिंदु के नियामक हैं
05:45View Solutionबिंदु (5,4,5) से रेखा x−11=y−22=z−33 की लम्बवत् दूरी ज्ञात कीजिए ।
10:51View SolutionThe distance of the point (1, 2, 1) from the line x−12=y−21=z−32 is
04:26View Solution