Consider a plane x+y−z=1 and point A(1,2,−3). A line L has the equation x=1+3r,y=2−randz=3+4r.
The coordinate of a point B of line L such that AB is parallel to the plane is Solution in Bengali
(a) (10,−1,15)
(b) (−5,4,−5)
(c) (4,1,7)
(d) (−8,5,−9)
The correct Answer is:d
The line x−13=y−2−1=z−34=r
Any point say B≡(3r+1,2−r,3+4r) (on the line L)
−−→AB=3r,−r,4r+6
Hence,
−−→AB is parallel to x+y−z=1
⇒ 3r−r−4r−6=0orr=−3
B is (−8,5,−9)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MATRIX-MATCH TYPE5videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - INTEGER TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE10videos
THREE-DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions291videos
THREE DIMENSIONAL GEOMETRY
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
Similar Questions
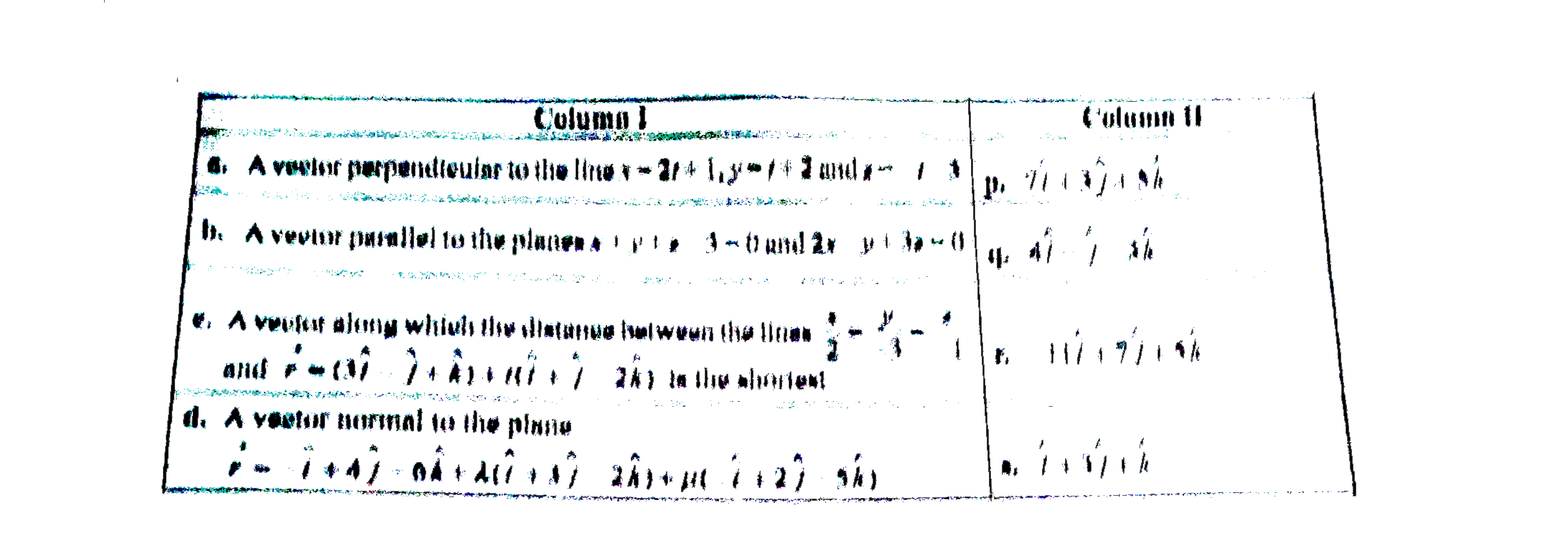
View SolutionFind the number of sphere of radius r touching the coordinate axes.
View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
07:53View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
04:16View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
02:40View SolutionLet the line L having equation x−12=y−35=z−13 intersects the plane P, having equation x−y+z=5 at the point A.
Statement-I Equation of the line L' thorugh the point A, lying in the plane P and having minimum inclination with line L is 8x+y−72−4=0=x−y+z−5
Statement-II Line L' must be projection of the line L in the plane P.04:29View Solutionसिद्ध कीजिए कि रेखाएँ x+1−3=y−32=z+21 और x1=y−7−3=z+72 समतलीय है। इनके प्रतिच्छेद बिन्दुओं के निर्देशांक तथा इन रेखाओं को रखने वाले समतल का समीकरण ज्ञात कीजिए।
06:12View SolutionLying in the plane x+y+z=6 is a line L passing through (1, 2, 3) and perpendicular to the line of intersection of planes x+y+z=6 and 2x−y+z=4, then the equation of L is
04:29View SolutionConsider a plane P:2x+y−z=5, a line L:x−32=y+1−3=z−2−1 and a point A(3,−4,1). If the line L intersects plane P at B and the xy plane at C, then the area (in sq. units) of ΔABC is
04:29View SolutionConsider a plane x+y−z=1 and point A(1,2,−3). A line L has the equation x=1+3r,y=2−randz=3+4r. The equation of the plane containing line L and point A has the equation
02:54View Solutionसमतल x+y−z=1 तथा बिंदु A(1,2,-3) पर विचार कीजिए।
एक रेखा L का समीकरण
x=1+3r
y=2−r
z=3+4r है।
रेखा L पर बिंदु B जो इस प्रकार है कि AB समतल के समांतर है, B के निर्देशांक है:
(i) 10,−1,15 (ii) −5,4,−5 (iii) 4,1,7 (iv) −8,5,−905:07View Solutionमाना एक समतल x+y−z=1 तथा एक बिन्दु A (1,2,-3) है। एक रेखा L के समीकरण x=1+3r,y=2−r तथा z=3+4r है
समतल का समीकरण जिसमें रेखा L तथा बिन्दुA का समीकरण है04:20View Solutionसमतल x+y−z=1 तथा बिंदु A(1,2,-3) पर विचार कीजिए।
एक रेखा L का समीकरण
x=1+3r
y=2−r
z=3+4r है।
रेखा L पर बिंदु B जो इस प्रकार है कि AB समतल के समांतर है, B के निर्देशांक है:
(i) 10,−1,15 (ii) −5,4,−5 (iii) 4,1,7 (iv) −8,5,−908:25View Solutionसमतल x+y−z=1 तथा बिंदु A(1,2,-3) पर विचार कीजिए।
एक रेखा L का समीकरण
x=1+3r
y=2−r
z=3+4r है।
रेखा L पर बिंदु B जो इस प्रकार है कि AB समतल के समांतर है, B के निर्देशांक है:
(i) 10,−1,15 (ii) −5,4,−5 (iii) 4,1,7 (iv) −8,5,−906:29View SolutionEquation of a plane through the line x−12=y−23=z−34 and parallel to a coordinate axis is
05:52View SolutionConsider a plane x+y−z= 1 and point A(1,2,−3). A line L has the equation x=1+3r,y=2−randz=3+4r
The equation of the plane containing line L and point A has the equation08:30View Solution