Question

Out of 100 students, 15 passed in English, 12 passed in Mathmatics, 8 in Science, 6 in English and Mathematics, 7 in Mathematics and Science , 4 in English and Science, 4 in all the three. Find how many passed
(i) in English and Mathematics but not in Science.
(ii) in Mathematics and Science but not in English.

Answer

(a) 2 (b) 3 ( c) 3 (d) 9

Explanation

Let M be the set of students who passed in Mathematics , E be the set of students who passed in English and S be the set of students who passed in Science

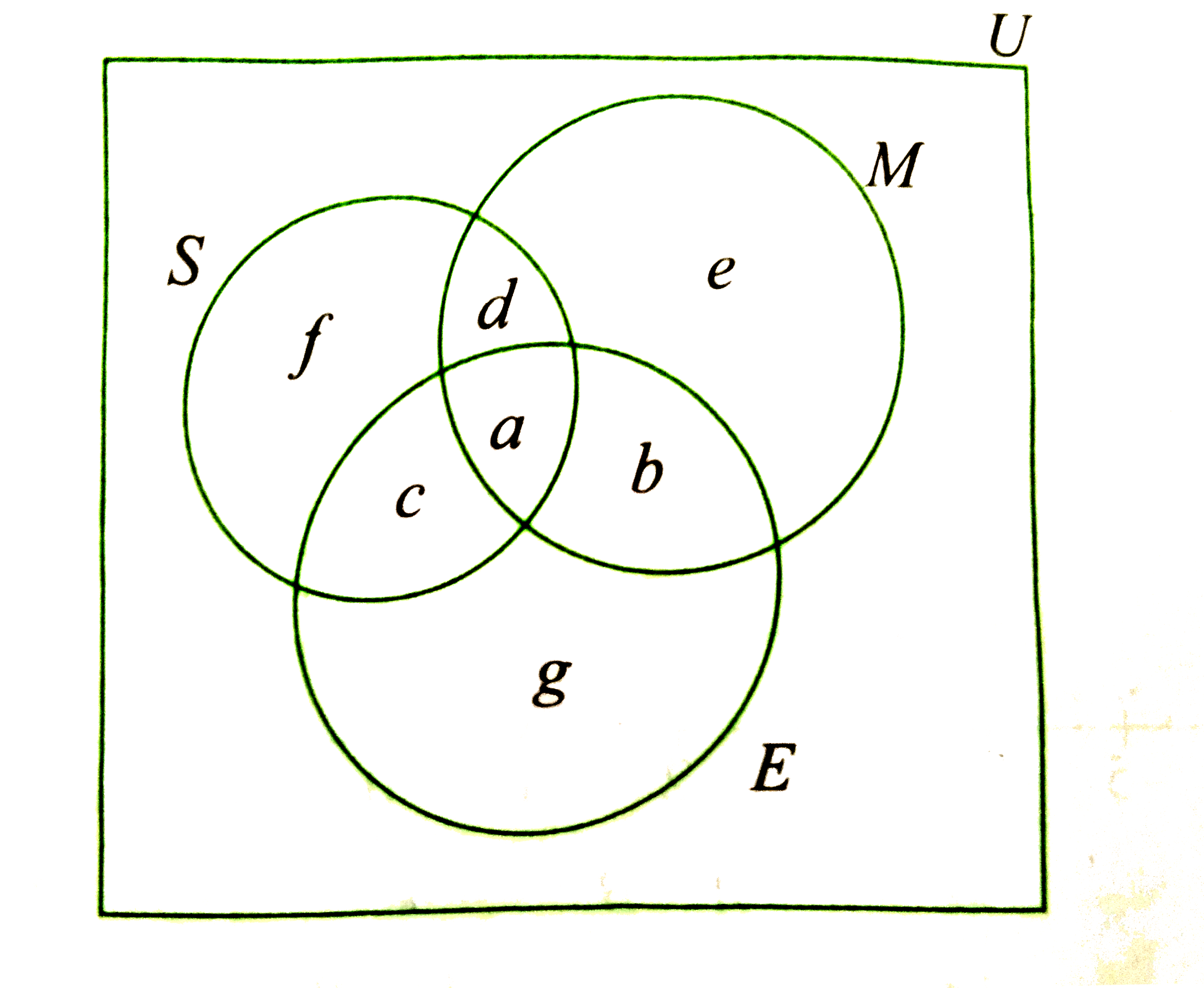
Given n( U)= 100
n( E) = 15 , n( M ) = 12 , n(s) = 8
` n( E cap M ) = 6 , n( M cap S) = 7 `
`n( E cap S ) = 4 and n( E cap M cap S ) = 4 `
From the Venn diagram , we have
`a= ( E cap M cap S ) = 4 and a+ d = n ( M cap S) = 7 rArr d= 3 `
`a +b =n(M cap E ) =6 " " rArr b= 2`
`a+ c =n( S cap E ) = 4 " " rArr c= 0 `
a+b+ d+ e= n( M)= 12
`rArr 4+2+3+e = 12 " " rArr e= 3`
a+b+c+g = 15
`rArr 4+2+0+g= n( E) = 15 rArr g= 9`
a+c+d+f= n(s)=8
`rArr 4+0+3+f= 8 " " rArr f= 1`
Number of students passed in
(a) English and Mathematics but not in Science = b= 2
( b) Mathematics and Science but not in English = d= 3
Mathmatics only = e= 3
( d) more than one subject =a+b+c+d+= 4+2+0+3=9