Draw the graph of f(x) maximum {2sinx,1−cosx},x∈(0,π). Also find the range of g(x) min {2sinx,1−cosx},x∈(0,π)Solution in Bengali
Let us first draw graphs of g1(x)=2sinx and g2(x)=1−cosx
g1(0)=g1(π)=0,g1(π/2)=2
g2(x)=sinx>0,∀x∈(0,π)
So g2'(x) is increasing.
g2(0)=0,g2(π/2)=1,g2(π)=2
Graph of functions are as shown in the following figure.
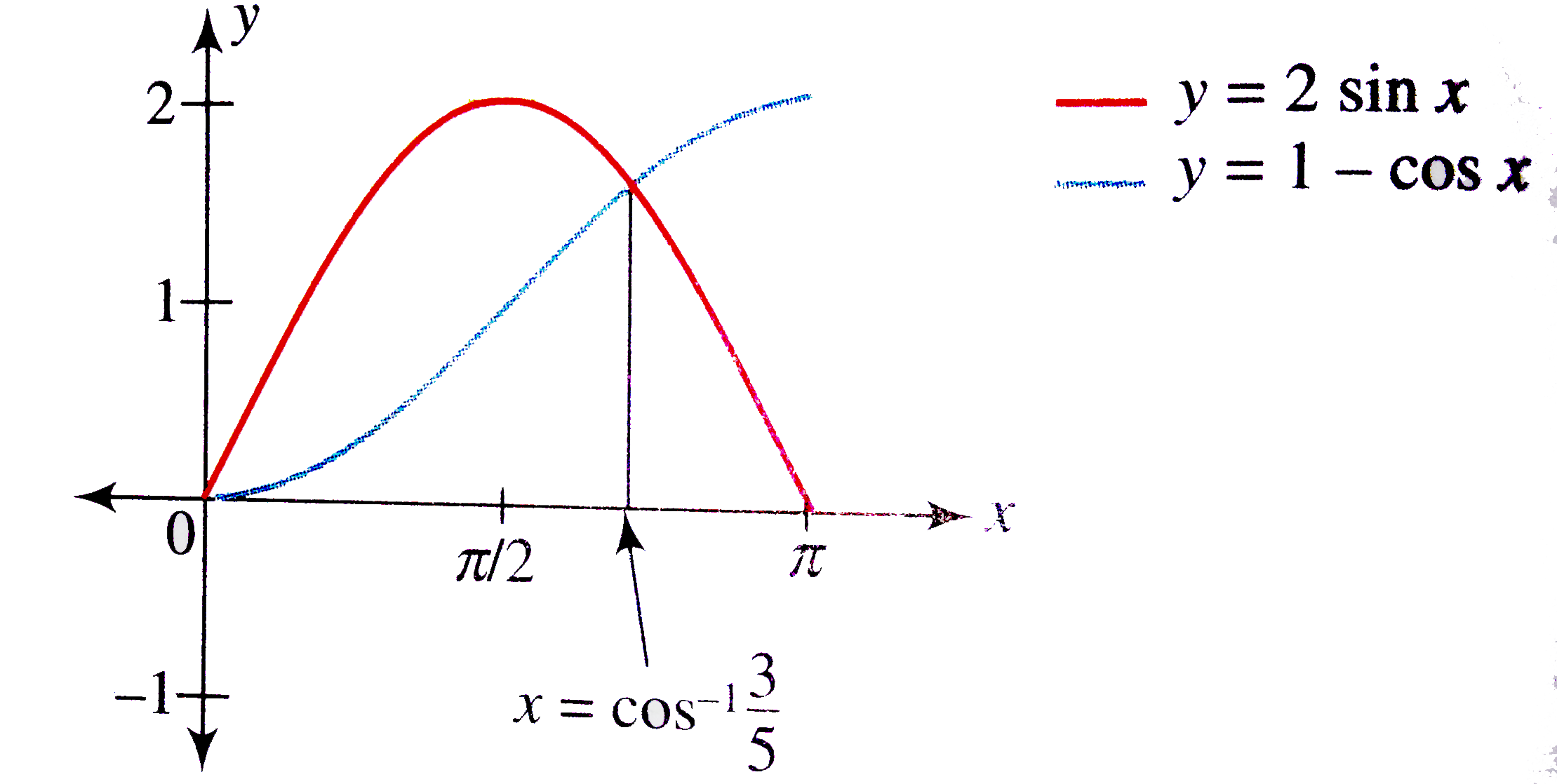
Curves y = 2 sin x and y = 1 - cos x intersect when
4sin2x=(1−cosx)2
⇒ 4(1+cosx)=(1−cosx)
⇒ 4+4cosx=1−cosx
⇒ cosx=−3/5
⇒ x=cos−1(−3/5)
∴ f(x)=⎧⎨⎩2sinx,0<x<π−cos−1351−cosx,π−cos−135<x<π
Also the range of g(x)=min{2sinx,1−cosx} is [0,1−coscos−1(−35)]≡[1,8/5].
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
07:20View SolutionDraw the graph of y=1(1/x).
01:38View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
02:38View SolutionShow that f(x)=sinx(1+cosx) is maximum at x=π3 in the interval [0,π].
13:06View SolutionStatement 1: Let f(x)=sin(cosx)∈[0,π2]. Then f(x) is decreasing in [0,π2] Statement 2: cosx is a decreasing function ∀x∈[0,π2]
10:56View SolutionIf 0
03:09View SolutionLet f(x)={x^(3)+x^(2)-10x,-1<=x<=0,sin x,0<=x<(pi)/(2),1+cos x,(pi)/(2)<=x<=pi then 'f(x) has
02:43View SolutionFind the area bounded by the curves y=(sin^(-1)(sin x)+cos^(-1)(cos x)) and y=(sin^(-1)(sin x)+cos^(-1)(cos x))^(2) for 0<=x<=2 pi
04:11View SolutionIf f(x)=(sqrt(cos((pi)/(2)-x)))/(1-cos(x+(pi)/(2))^((1)/(3))) and g(x)=(1)/(sqrt([sin x])) then range of g(x)-f(x) contains
View SolutionShow that f(x)=sinx(1+cosx) is maximum at x=π3 in the interval [0, π] .
05:23View Solutionint_ (0) ^ ((pi) / (2)) (sin x) / (sin x + cos x) dx = int_ (0) ^ ((pi) / (2)) (cos x) / (sin x + cos x) dx = int_ (0) ^ ((pi) / (2)) (dx) / (1 + cot x) = int_ (0) ^ ((pi) / (2)) (dx) / ( 1 + time x) = (pi) / (4)
02:52View SolutionDraw the graph of f(x) maximum {2sinx,1−cosx},x∈(0,π). Also find the range of g(x) min {2sinx,1−cosx},x∈(0,π)
07:46View Solution(i) ∫π0xdx1+sinx का मान ज्ञात कीजिये।
(ii) ∫π/20sinx−cosx1+sinxcosxdx का मान ज्ञात कीजिये।02:56View Solution∫π/20sinx−cosx1+sinxcosxdxका मान ज्ञात कीजिएः
View Solution∫π/20sinxcosx(1+2sinx)(1+sinx)dx=
06:40View SolutionIf f'(x)=3x2sin(1x)−xcos(1x),x≠0,f(0)=0 then the value of f(1π) is
03:25View Solution

