Find the ratio of the areas of two regions of the curve C1≡4x2+π2y2=4π2 divided by the curve C2≡y=−(sgn(x−π2))cosx (where sgn (x) = signum (x)). Solution in Bengali
4x2+π2y2=4π2
∴ C1:x2π2+y24=1, which is an ellipise.
Curve C2:y=−sgn(x−π2)cosx
=⎛⎜
⎜⎝−cosx,x>π2cosx,x<π20,x=π2
Graphs of C1 and C2 are as shown in the following figure.
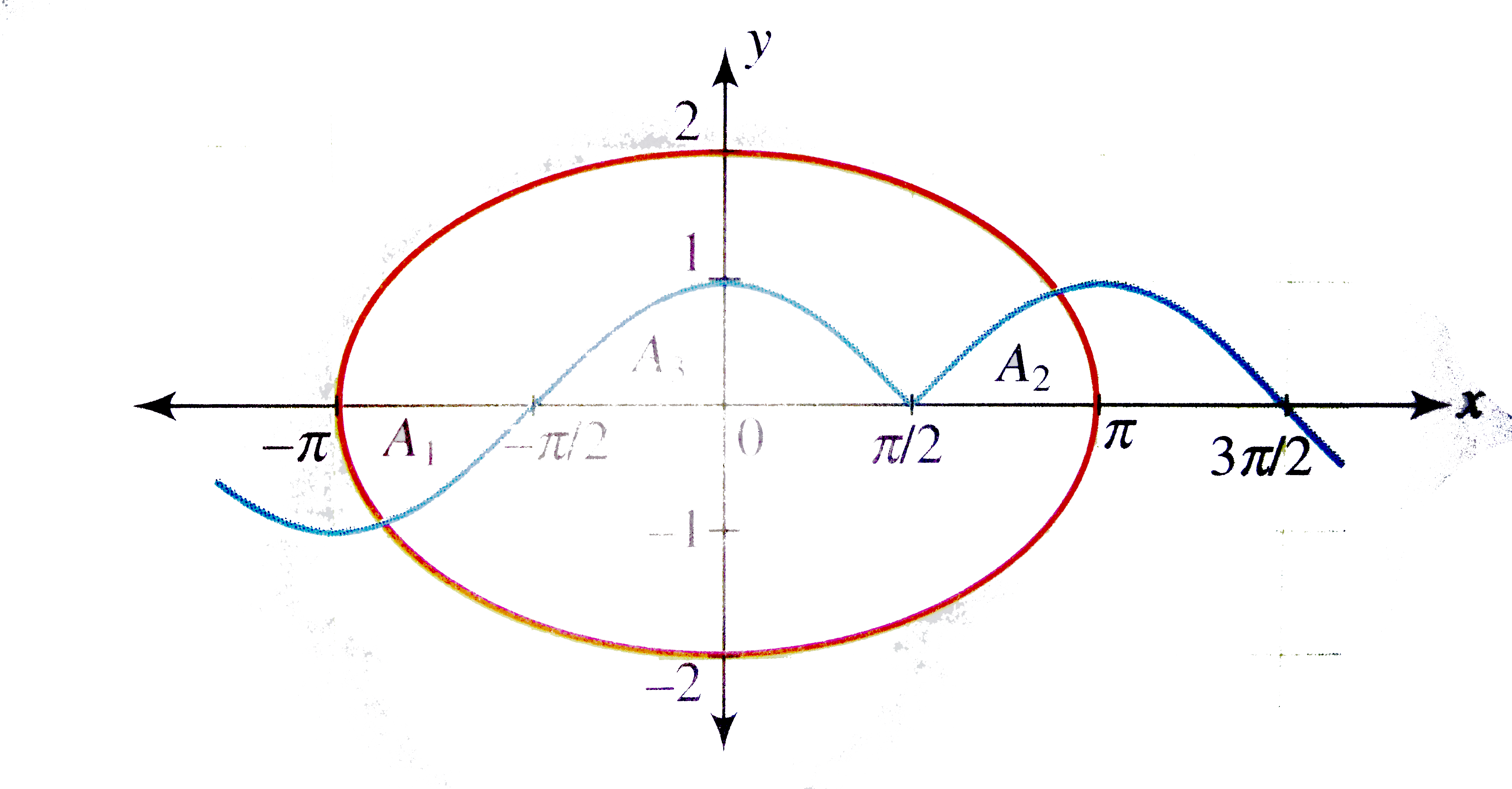
From the symmetry of the curves, the areas of regions A1 and A2 are equal.
Area of ellipse is π(π)(2)=2π2.
Area of ellipse above the x - axis is π2.
Now the area bounded by y = cos x and the x - axis (A3) is 2 sq. units.
So the area of the portion of the ellipse above the curve C2 is π2−2 (as the areas of regions A1 and A2 are same)
So the area of the portion of the ellipse below the curve C2 is π2+2.
Hence the required ratio is π2−2π2+2
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
05:01View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
02:39View SolutionIf sgn(x−2x+1)≤x−12. then x may belongs to (where sgn() represents signum fuction)
02:18View SolutionFind the ratio of the areas of two regions of the curve C1≡4x2+π2y2=4π2 divided by the curve C2≡y=−(sgn(x−π2))cosx (where sgn (x) = signum (x)).
02:22View SolutionThe ratio of the areas of two regions of the curve C1≡4x2+π2y2=4π2 divided by the curve C2≡y=−(sgn(x−π2))cosx (where sgn (x) = signum (x)) is
08:42View SolutionFind the area of the region bounded by the curve y=sinx, the lines x=−π2,x=π2 and X- axis.
04:58View SolutionIf f(x)=sgn(cos2x−2sinx+3), where sgn () is the signum function, then f(x)
12:56View Solutionदो वक्र c1=y2=4x व c2=x2+y2−6x+1=0 हैं, तब-
16:09View Solutionप्रथम चतुर्थांश में वक्रों x2+y2=π2 एवं y=sinx से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए ।
04:02View SolutionConsider the curves C1=y−4x+x2=0 and C2=y−x2+x=0
The ratio in which the x-axis divide the area of the region bounded by the curves C1=0 and C2=0 is03:55View SolutionConsider the curves C1=y−4x+x2=0 and C2=y−x2+x=0
The raio in which the line y = x divide the area of the region bounded by the curves C1=0 and C2=0 is02:07View SolutionThe line y=x+1 divided the area the curves y=cosx,[−π2,π2] and the x-axis into two regions which are in the ratio
03:00View SolutionFind the ratio of the areas of two regions of the curve C1≡4x2+π2y2=4π2 divided by the curve C2≡y=−(sgn(x−π2))cosx (where sgn (x) = signum (x)).
07:09View SolutionThe ratio of the areas of two regions of the curve C1≡4x2+π2y2=4π2 divided by the curve C2≡y=−(sgn(x−π2))cosx (where sgn (x) = signum (x)) is
07:35View SolutionFind the area of the region bounded by the curve y=sinx,x=π2andx=3π2.
05:00View Solution

