Find the ratio of the areas of two regions of the curve $C_{1} \equiv 4 x^{2} + π^{2} y^{2} = 4 π^{2}$ divided by the curve $C_{2} \equiv y = - (s g n (x - \frac{π}{2})) cos x$ (where sgn (x) = signum (x)).

Text Solution

Verified by Experts

$4 x^{2} + π^{2} y^{2} = 4 π^{2}$
$∴$ $C_{1} : \frac{x^{2}}{π^{2}} + \frac{y^{2}}{4} = 1$ , which is an ellipise.
Curve $C_{2} : y = - s g n (x - \frac{π}{2}) cos x$
$= ⎛ ⎜ ⎜ ⎝ \begin{matrix} - cos x, & x > \frac{π}{2} cos x, & x < \frac{π}{2} 0, & x = \frac{π}{2} \end{matrix}$
Graphs of $C_{1}$ and $C_{2}$ are as shown in the following figure.

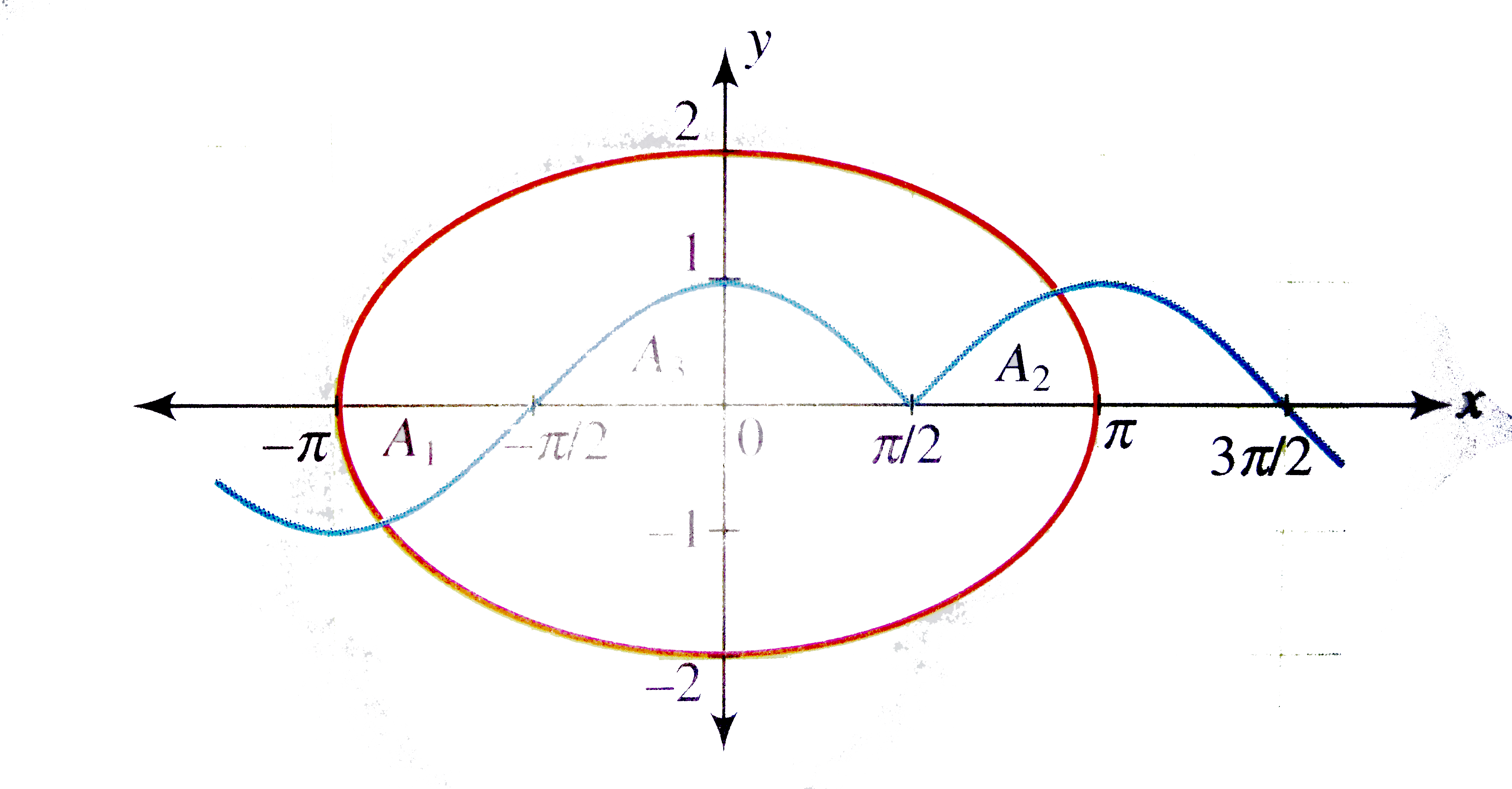
From the symmetry of the curves, the areas of regions $A_{1}$ and $A_{2}$ are equal.
Area of ellipse is $π (π) (2) = 2 π^{2}$ .
Area of ellipse above the x - axis is $π^{2}$ .
Now the area bounded by y = cos x and the x - axis $(A_{3})$ is 2 sq. units.
So the area of the portion of the ellipse above the curve $C_{2}$ is $π^{2} - 2$ (as the areas of regions $A_{1}$ and $A_{2}$ are same)
So the area of the portion of the ellipse below the curve $C_{2}$ is $π^{2} + 2$ .
Hence the required ratio is $\frac{π^{2} - 2}{π^{2} + 2}$

The ratio of the areas of two regions of the curve $C_{1} \equiv 4 x^{2} + π^{2} y^{2} = 4 π^{2}$ divided by the curve $C_{2} \equiv y = - (s g n (x - \frac{π}{2})) cos x$ (where sgn (x) = signum (x)) is
A $\frac{π^{2} - 2}{π^{2} - 2 \sqrt{2}}$
B $\frac{π^{2} + 2}{π^{2} - 2 \sqrt{2}}$
C $\frac{π^{2} + 6}{π^{2} + 3 \sqrt{2}}$
D $\frac{π^{2} - 1}{π^{2} - \sqrt{2}}$