A spherical ballon of radius r while floating in the sky, makes an angle α in the eye of viewer. If the angle of elevation of the centre of the ballon in the eye of the viewer be β, show that the altitude of the centre of the ballon from the ground is rcosecα2sinβ.Solution in Bengali
Let O be the centre of the balloon of radius which subtends an angleα at E , the eyes of observer .
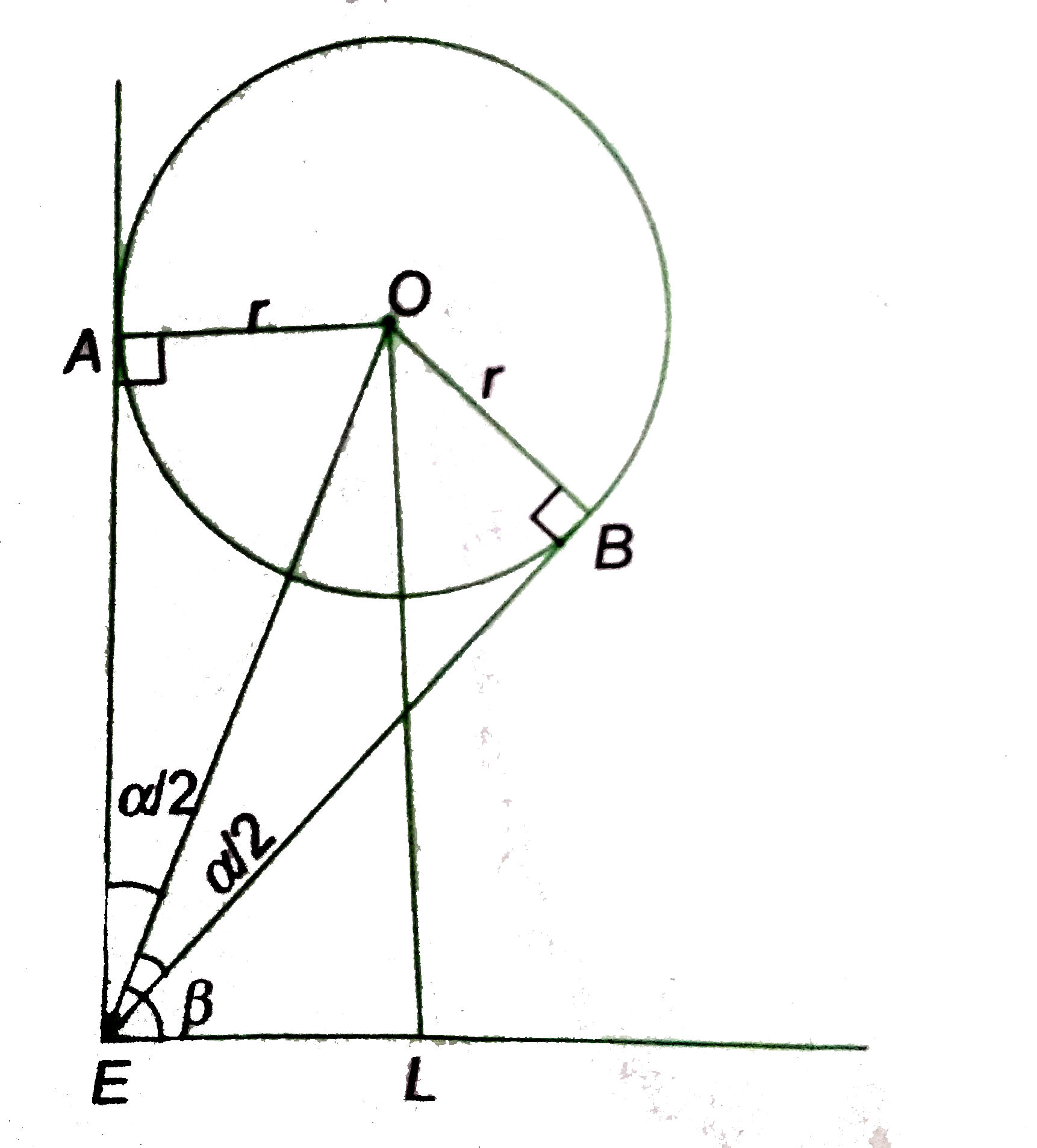
EA and EB are the tangents to the balloon .
∴∠OEA=∠OEB=α/2
Let the height OL of the balloon be h .
In Δ OLE ,
h=OE sinbeta
=rcosec(α/2)sinβ ( in triangle OBE)
=rsinβsin(α/2)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Exercises18videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
Similar Questions
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30o with horizontal, then the length of the wire is (a) 12 m (b) 10 m (c) 8 m (d) 6 m
05:03View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
04:26View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
04:09View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
05:35View SolutionA round balloon of radius r subtends an angle alpha at the eye of the observer while the angle of elevation of its centre is beta Prove that the height of the centre of the balloon is r sin beta cos ec[(alpha)/(2)]
04:50View SolutionA round balloon of radius r subtends an angle alpha at the eye of the observer while the angle of elevation of its centre is beta. Prove that the height of the centre of the balloon is r sin(beta)cos ec(alpha)/(2)
08:16View SolutionA round balloon of radius r subtends an angle at the eye of the observer while the angle of elevation of its centre is β. Prove that the height of the centre of the balloon is rsinβcosecα2.
04:29View SolutionA spherical ball of diameter d subtends an angle alpha at a man's eye when the elevation of its centre is beta ,then the height of the centre of the ball is (1)/(2)d sin beta cos ec((alpha)/(2))
03:21View SolutionA balloon of radius r subtends an angleα at the eyes of an observer and the center of balloon from the eye is β . Find the height of the center of the balloon from the eye of observer .
07:56View Solutionएक गोलाकार गुब्बारा जिसकी त्रिजया r है, दर्शक की आंख पर α कोण बनाता है और इसके केन्द्र का आंख से उन्नयन कोण β हैं सिद्ध कीजिए कि गुब्बारे के केंद्र की पृथ्वी से ऊंचाई rsinβcosecα2 है।
02:27View SolutionA spherical balloon of radius r subtends an angle α at the eye of anb observer. If the angle of elevation of the cerntre of the balloon be β, then prove that the height of the balloon is
r cosecα2sinβ.05:37View Solutionत्रिज्या 'r' का एक गोलाकार एक प्रेक्ष्क की आँख पर कोण अंतरित करता है यदि इसके केंद्र का उनयन कोण β है तो सिद्ध कीजिएः की गुबबरेह के केंद्र की उचाई rsinβcosecα2 है
03:42View SolutionA spherical balloon of radius 50 cm, subtends an angle of 60∘ at a man's eye when the elevation of its centre if 45∘. Then the height of the centre of the ballon is
View SolutionA round balloon of radius 'r' subtends an angle α at the eye of the observer, while the angle of elevation of its centre is β. Find the height of the centre of balloon.
04:55View SolutionA round balloon of radius r subtends an angle a at the eye of the observer while the angle of elevation of its centre is p. Prove that the height of the centre of the balloon B is r sin β cosec α2.
05:08View Solutionएक r त्रिज्या का गोलीय गुब्बारा , किसी प्रेक्षक की आँख पर α कोण बनाता है। यदि गुब्बारे के केंद्र का उन्नयन कोण β हो, तो गुब्बारे के केंद्र की ऊंचाई है
10:58View Solution

