The length of the shadow of a pole inclined at 10∘ to the vertical towards the sun is 2.05 metres, when theelevation of the sun is 38∘. Then, find the length of the pole.Solution in Bengali
2.05sin42∘sin38∘
2.05sin42∘cos42∘
2.05sin38∘sin42∘
2.05sin42∘sin38∘
Let PO be the tower and OS be its shadow .
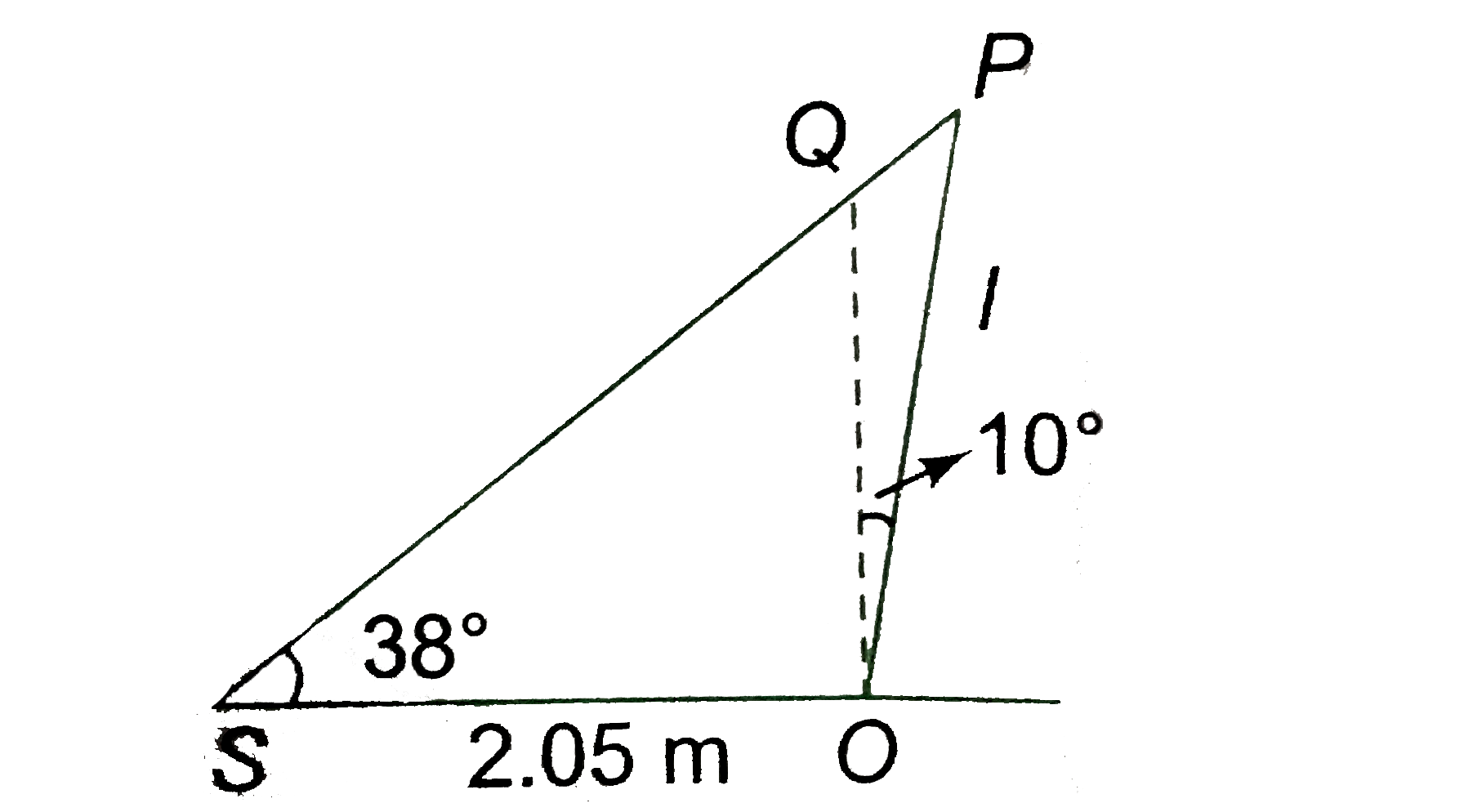
In triangle SOP , using sine rule ,
lsin38∘=2.05sin(∠SPO) ...(1)
∠SPO=180∘−38∘−90∘−10∘=42∘
So from (1), l=2.05sin38∘sin42∘
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
03:17View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
01:24View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
01:16View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
03:08View SolutionThe length of the shadow of a pole inclined at 10^(@) to the vertical towards the sun is 2.05 metres,when theelevation of the sun is 38^(@) Then,find the length of the pole.
03:38View SolutionFind the angle of elevation of the sun (sun’s altitude) when the length of the shadow of a vertical pole is equal to its height.
03:54View SolutionIf the height of a pole is 2√3 metres and the length of its shadow is 2 metres, find the angle of elevation of the sun.
07:14View SolutionThe shadow of a pole is 9 m long when the angle of elevation of the sun is 30∘.Find the length of shadow when the angle fo elelvation of the sun is 60∘.
04:53View SolutionThe length of the shadow of a pole inclined at 10∘ to the vertical towards the sun is 2.05 meters, when the elecation of the sun is 38∘. Then, the length of the pole.
04:59View SolutionThe length of shadow of a pole is equal to the length of the pole, then the angle of the elevation of the Sun is …………
03:03View SolutionThe length of the shadow of a pole inclined at 10∘ to the vertical towards the sun is 2.05 metres, when theelevation of the sun is 38∘. Then, find the length of the pole.
02:44View SolutionFind the angle of elevation of the sun (sun’s altitude) when the length of the shadow of a vertical pole is equal to its height.
01:53View Solutionजब सूर्य का उन्यन कोण 38∘ है तो ऊर्ध्वाधर से सूर्य की और 10∘ के कोण पर झुके एक खम्बे की छाया की लम्बाई 2.05 मीटर है। खम्बे की ऊँचाई है।
01:39View SolutionThe shadow of a pole is 9m long when the angle of elevation of the sun is 30∘. Find the length of the shadow when the angle of elevation of the sun is60∘.
View SolutionA vertical pole is 10 mts. High. The length of its shadow is 10√3 mts. What is the angle of elevation of the sun?
View Solution

