A flagstaff stands in the centre of a rectangular field whose diagonal is 120 m. It subtends angles of 15∘ and 45∘ at the midpoints of the sides of the field. The height of the flagstaff isSolution in Bengali
20m
30√2+√3m
30√2−√3m
40m
Let OP be the flagstaff of height 'h' standing at the centre O of the rectengular field ABCD subtending angless 15∘and45∘ at E and F ,respectivily ,
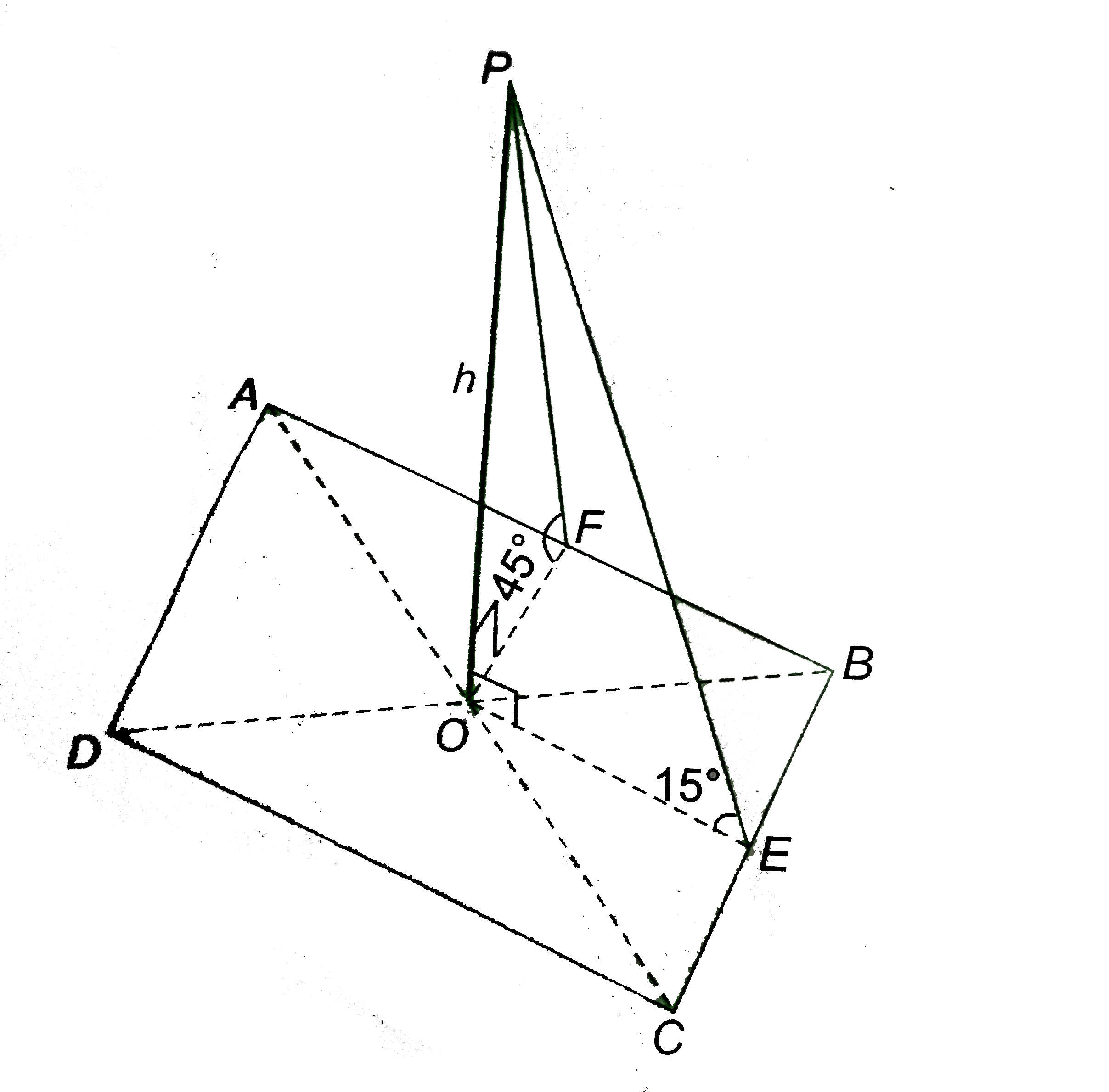
In triangle POE , OE =hcot15∘=h(2+√3)
In triangle POF ,OF = hcot45∘=h
⇒EF=√h2=(2+√3)2h2
2h√2+√3
Triangles ACB and FEB are similar .
so, AC =2EF
⇒120=4h√(2+√3) ,
⇒h=30√2+√3=30√2−√3
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives3videos
HIGHT AND DISTANCE
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE2videos
HYPERBOLA
Similar Questions
A bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
14:07View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
08:03View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
03:48View SolutionA flagstaff stands on the top of a vertical tower. It is found that the flagstaff subtends the same angle alpha at two points , 2d apart, on a straight line through the base of the tower on the horizontal plane. Also the flagstaff subtends an angle beta at the midpoint of these two points find the value of
05:34View SolutionA temple and a flagstaff surmounted at its top, each subtends equal angle of 30∘ at a point on the ground. If the height of the temple is 10 m, find the height of the flagstaff.
01:09View SolutionA flagstaff stands in the centre of a rectangular field whose diagonal is 120 m. It subtends angles of 15∘ and 45∘ at the midpoints of the sides of the field. The height of the flagstaff is
04:37View SolutionThe angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45∘. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60∘, then find the height of the flagstaff. [Use √3=1.732.]
View SolutionAt a distance 12 metres from the foot A of a tower AB of height 5 metres, a flagstaff BC on top of AB and the tower subtend the same angle. Then, the height of flagstaff is
05:22View SolutionA vertical flagstaff stands on a horizontal plane. From a point 100 m from its foot, the angle of elevation of its top is found to be 45∘. Find the height of the flagstaff.
06:29View SolutionAt a distance d from the foot of tower AB of height h metres, a flagstaff BC (surmounted on the tower) and the tower subtend equal angles. Then the height of the flagstaff is :
02:44View SolutionA flagstaff 10 m high stands at the centre of a equilateral triangle, which is horizontal. At the top of the flagstaff each side subtends at an angle of 60°. The length of each side of the triangle is
03:03View SolutionA flagstaff stands in the centre of a rectangular field whose diagonal is 120 m. It subtends angles of 15∘ and 45∘ at the midpoints of the sides of the field. The height of the flagstaff is
04:58View SolutionAt a distance 12 metres from the foot A of a tower AB of height 5 metres, a flagstaff BC on top of AB and the tower subtend the same angle. Then, the height of flagstaff is
09:26View SolutionA tower of height 5m and a flagstaff on top of the tower subtend equal angles at a point on the ground, distance 13m from the base of the tower. The height of the flagstaff is
View Solution

