Question

Sketch the graph of the following functions $y=f\left(x\right)$ and find the number of real roots of the corresponding equation $f\left(x\right)=0$.
$\left(i\right)f\left(x\right)=2x^3-9x^2+12x-(9/2)\left(ii\right)f\left(x\right)=2x^3-9x^2+12x-3$

Explanation

(i) We have `y=f(x)=2x^(3)-9x^(2)+12x-(9//2)`
`:. f'(x)=6x^(2)-18x+12=6(x^(2)-3x+2)=6(x-1)(x-2)`
Now `f'(x)=0 rArr x=1 and x=2`
The sign scheme of `y=f'(x)` is as follows.

So `x=2` is the point of minima and `x=1` is the point of maxima.
`f(1)=2-9+12-(9//2) gt 0`
and `f(2)=16-36+24-(9//2) lt 0`
Hence the graph of the function `y=f(x)` is as shown in the following figure.

As shown in the figure, the graph cute the x-axis at three distinct points.
Hence the equation `f(x)=0` has three distinct roots.
(ii) We have `y=f(x)=2x^(3)-9x^(2)+12x-3`
`f'(x)=0 rArr x=1` and `x=2`
Also `f(1)=2-9+12-3 = 2 "and" f(2) = 16-36+24-3=1`
Hence the graph of `y=f(x)` is as shown in the following figure.

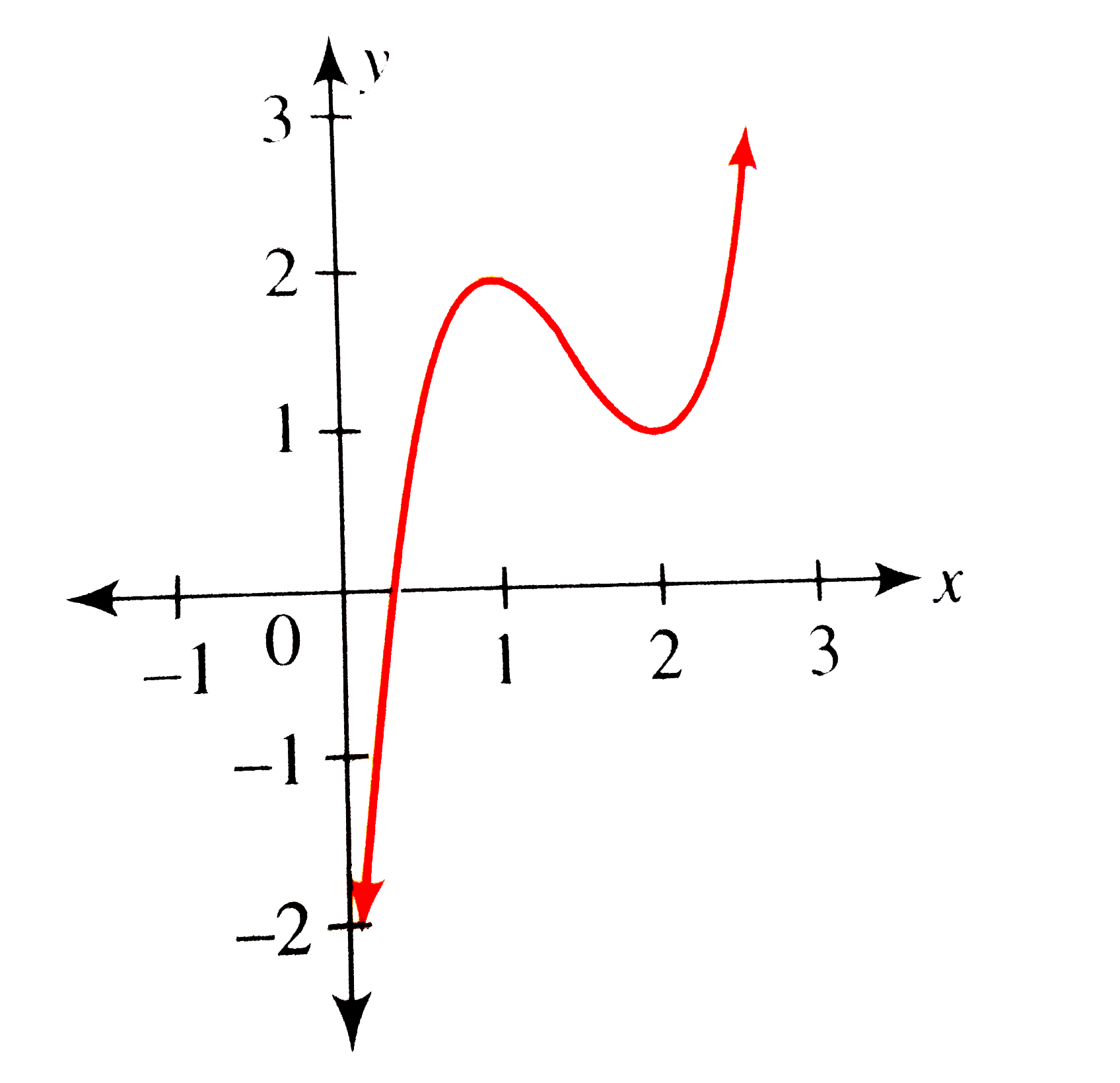
Thus, from the graph we can see that `f(x)=0` has only one real root, though `y=f(x)` has two turning points.