(a) Draw the graph of f(x)==⎧⎪
⎪⎨⎪
⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
(b) Sketch the region y≤−1.
(c) Sketch the region |x|<3.
Text Solution
(a) f(x)==⎧⎪
⎪⎨⎪
⎪⎩1,|x|≥11n2,1n<|x|<1n−1,n=2,3,...0,x=0
=⎧⎪
⎪
⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪
⎪
⎪⎩1,x≤−1orx≥114,x∈(−1,−12)∪(12,1)19,x∈(−12,−13)∪(13,12)...
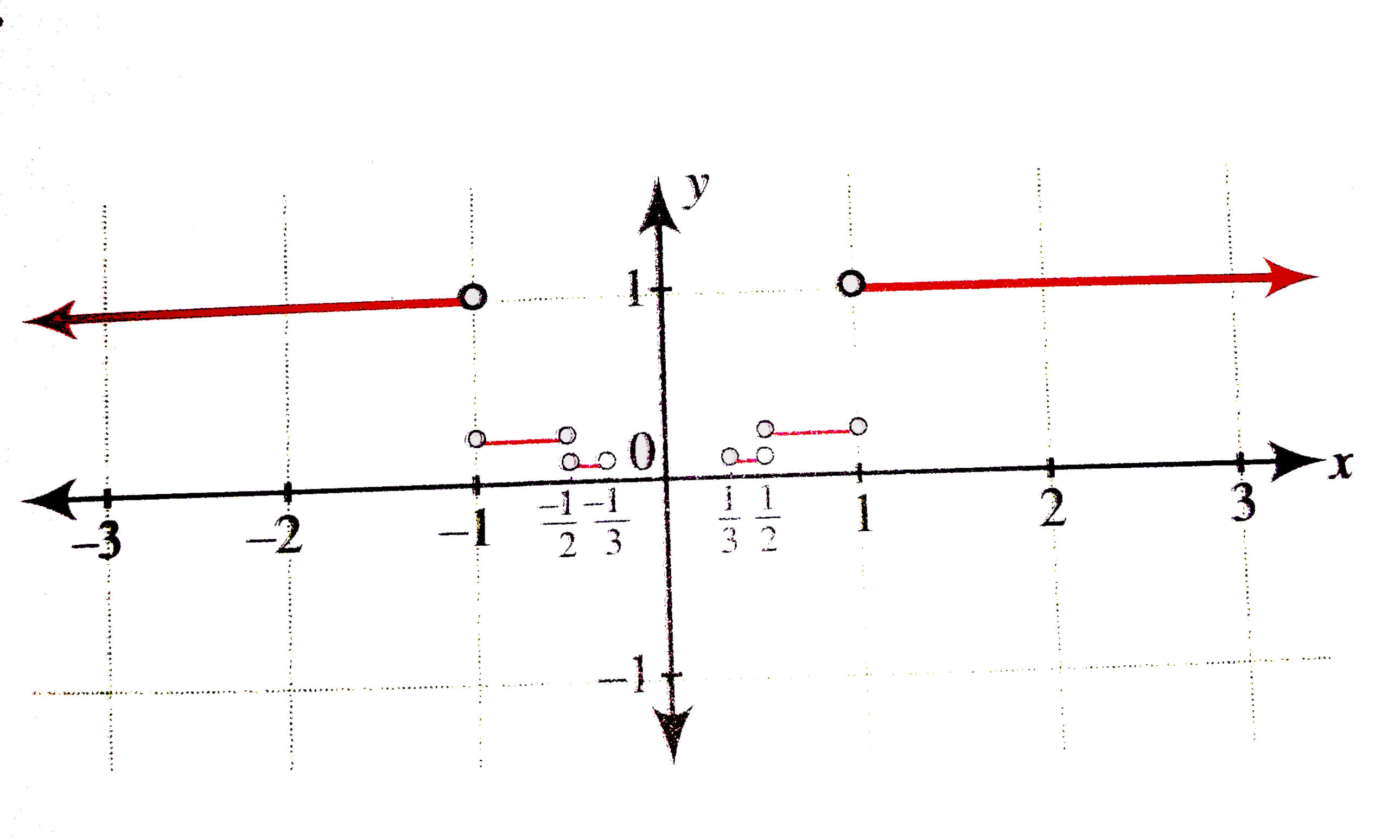
(b) y≤−1
For y≤−1, first draw the line y=−1. All the points satisfying y≤−1 have ordinate greater than, or equal to, -1, i.e. all the points lying on or below the line y=−1.
The region is as shown in the following region.

(c ) |x|<3
So −3<x<3, i.e. all points have abscissae lying between -3 and 3. Hence all the points lying between the lines x=−3andx=3.

|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One or More
The function f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩1|x|≤11n21n≤|x|<1n−1,n=2,3,...0x=0
Ais discontinuous at infinte pointsBis continuous everywhereCis discontinuous only at x=1n,n∈Z−{0}Dnone of these - Question 2 - Select One
Let f(x)={2x+a,x≥−1bx2+3,x<−1
and g(x)={x+4,0≤x≤4−3x−2,−2<x<0
If a=2andb=3, then the range of g(f(x)) isA(−2,8]B(0,8]C[4,8]D[−1,8] - Question 3 - Select One
If f(x)=⎧⎨⎩x, for 0≤x<121−x, for 12≤x<1 , then
Alimx→1−2f(x)=−12Blimx→1+2f(x)=−12Cf is continuous at x=12Df is discontinuous at x=12
Let f(x)={2x+a,x≥−1bx2+3,x<−1
and g(x)={x+4,0≤x≤4−3x−2,−2<x<0
If a=2andb=3, then the range of g(f(x)) isView SolutionDraw the graph of f(x)={(x−2n, 2n≤x<2n+1),( where n∈Z. Is f(x)),(12, 2n+1≤x<2n+2)
periodic? If yes, what is its period?View SolutionThe function f(x)=⎧⎪⎨⎪⎩5x−4 for 0<x≤14x2−3x for1<x<23x+4forx≥2is
View SolutionLet the function f is defined as follows
f(x)={12n,12n+1<x≤12n,n=0,1,2,...0else
Then,∫−10f(x)dx isView SolutionThe function f(x)=⎧⎪⎨⎪⎩5x−4 for 0<x≤14x2−3x for1<x<23x+4forx≥2is
View Solution

