Question

Sketch the region satisfying $\left|x\right|<\left|y\right|$.

Explanation

`|x| lt |y|`
`therefore " " ={{:(x lt y",",, xgt0", " y gt 0), (x lt y",",, x gt 0", " y lt 0), (-x lt y ",",, x lt 0", "y gt 0),(-xlt -y or y lt x",",, x lt 0", " y lt 0):}`
For `x, y gt 0 and x lt y`, we have the following region in the `1^(st)` quadrant lying to the left of the line `x=y`.

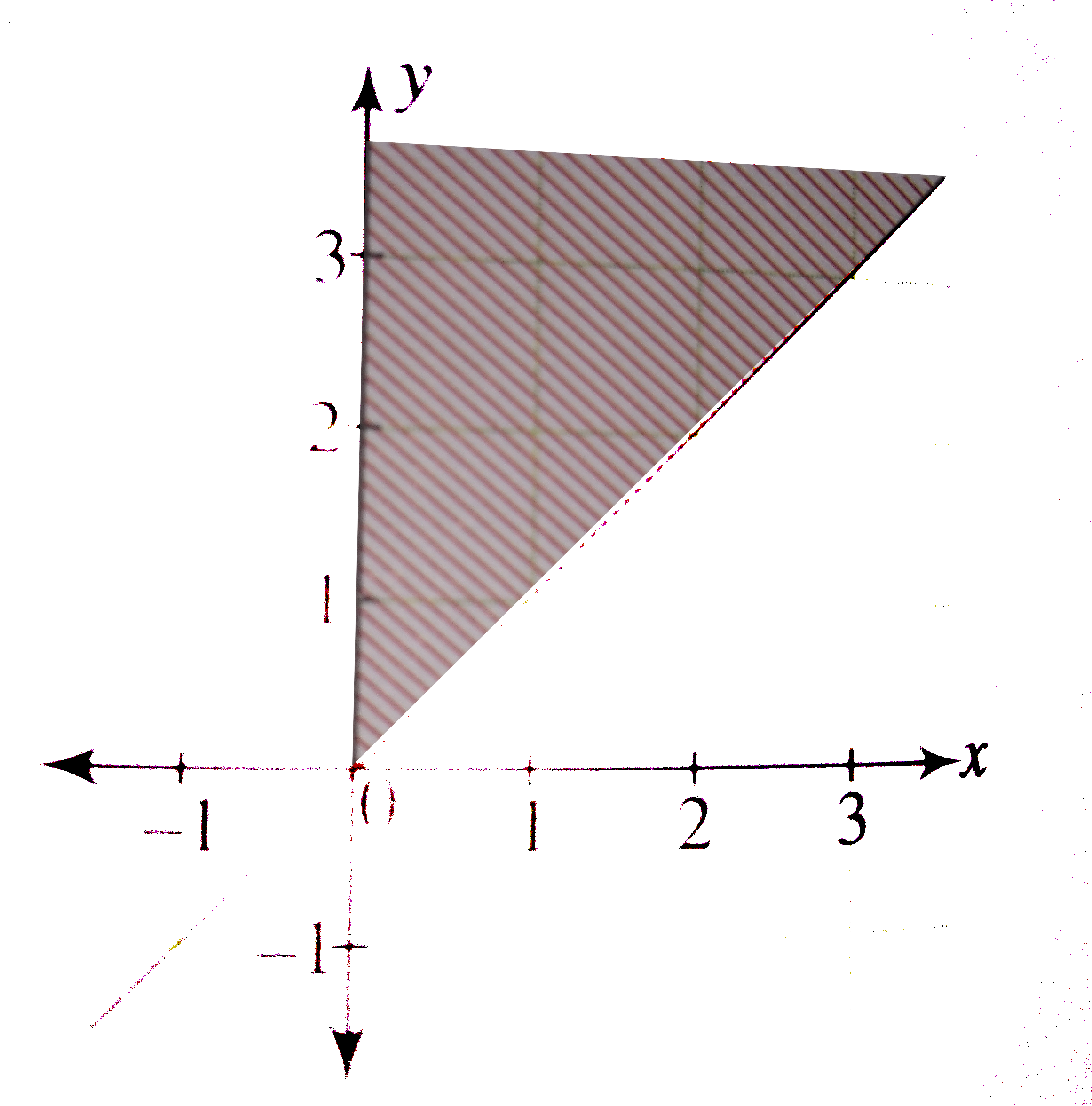
For `x, y lt 0 and x gt y`, we have the following region in the `3^(rd)` quadrant lying to the right of the line x=y.

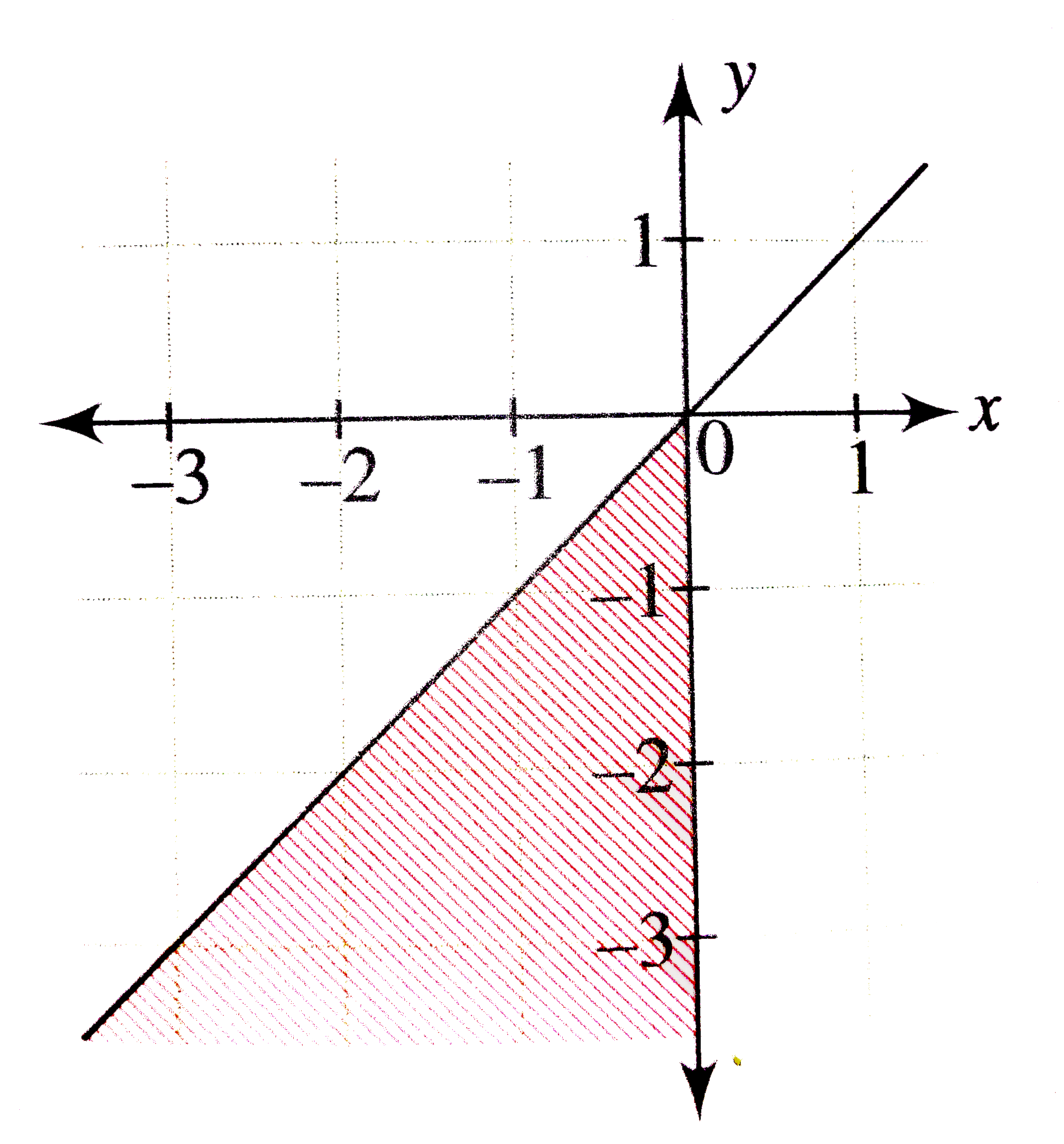
Similarly for `ylt 0 lt x and x lt -y`, we have the region in the `4^(th)` quadrant to the left of the line x= -y.
For `x lt 0 lt y and -x lt y`, we have the region in the `2^(nd)` quadrant to the right of the line x=-y.
Combining all four regions, we have the region as shown in the adjacent figure.