Match the following lists:
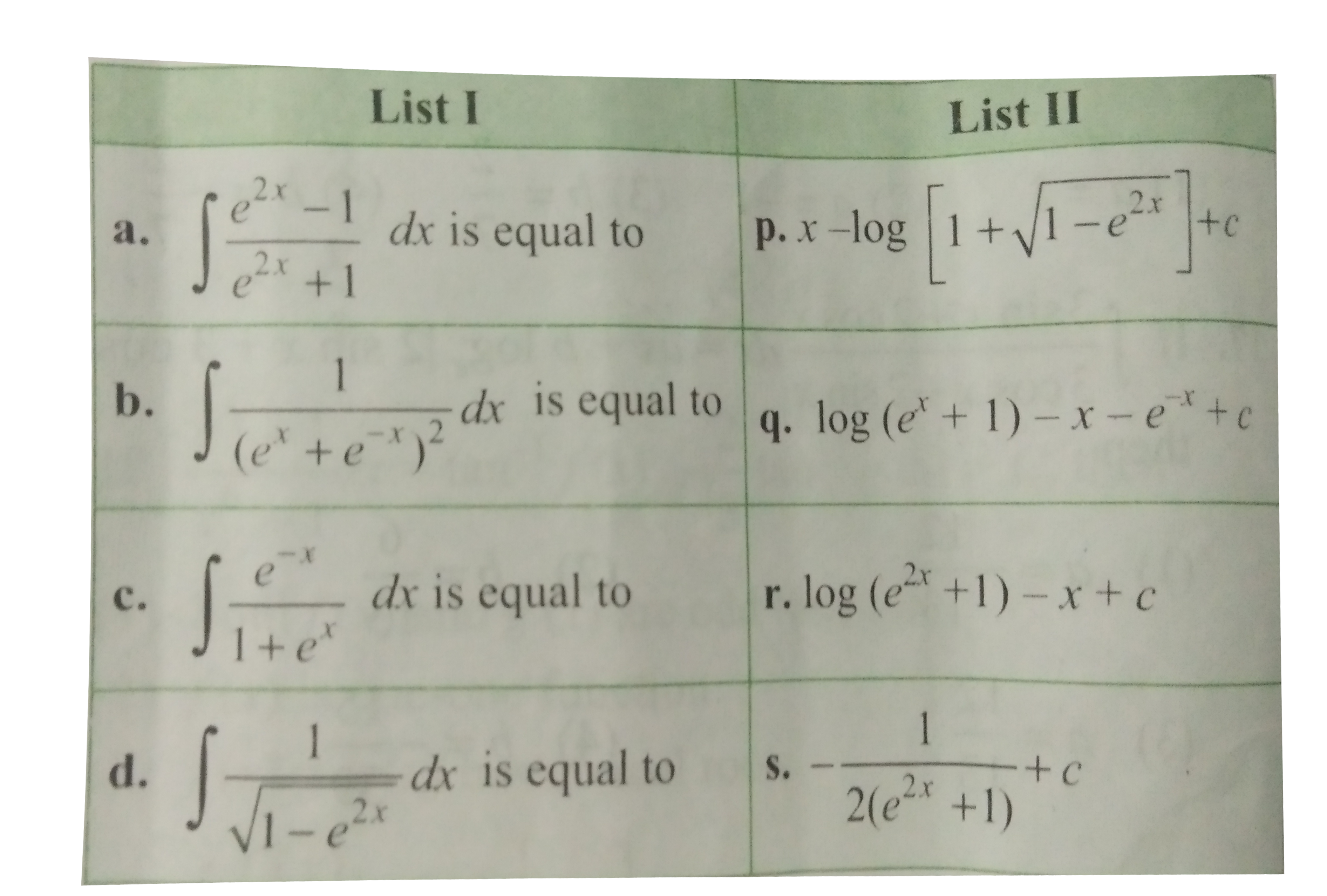Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $a \to r; b ⊤; c \to s; d t o q$

$lim n \to \infty ⎡ ⎢ ⎢ ⎣ \frac{\int_{0}^{2} {(1 + \frac{t}{n + 1})}^{n} d t}{n + 1} ⎤ ⎥ ⎥ ⎦ = lim n \to \infty {[{(1 + \frac{t}{n + 1})}^{n - 1}]}_{0}^{n - 1}$
$= lim n \to \infty {(1 + \frac{2}{n + 1})}^{n + 1} - 1$
$= e^{2} - 1$
$f' (x) = f (x) \Rightarrow f (x) = C e^{x}$ and since $f (0) = 1, 1 = f (0) = C$
Therefore $f (x) = e^{x}$ and hence $g (x) = x^{2} - e^{x}$ .
Thus, $\int_{0}^{1} f (x) g (x) d x = \int_{0}^{1} (x^{2} e^{x} - e^{2 x}) d x$
$= x^{2} e^{x} ∣_{0}^{1} - 2 \int_{0}^{1} x e^{x} d x = \int_{0}^{1} (x^{2} e^{x} - e^{2 x}) d x$
$= x^{2} e^{x} {∣ ∣ ∣ ._{0}^{1} - 2 \int_{0}^{1} x e^{x} d x - \frac{e^{2 x}}{2} ∣ ∣ ∣}_{0}^{x}$
$= (e - 0) - 2 x e^{x} {∣ ∣ ._{0}^{1} + 2 e^{x} ∣ ∣}_{0}^{x} + 2 e^{x} ∣_{0}^{1} - \frac{1}{2} (e^{2} - 1)$
$= (e - 0) - 2 e + 2 e - 2 - \frac{1}{2} (e^{2} - 1)$
$= e - \frac{1}{2} e^{2} - \frac{3}{2}$
$I = \int_{0}^{1} e^{e^{x}} (1 + x e^{x}) d x$
Let $e^{x} = t$
$∴ \int_{1}^{e} (1 + t log t) \frac{d t}{t} \int_{1}^{e} e^{t} (\frac{1}{t} + log t) d t$
$= {[e^{t} log t]}_{1}^{t} = e^{e}$
d. $L = lim k \to 0 \frac{\int_{0}^{k} {(1 + sin 2 x)}^{\frac{1}{x}} d x}{k}$ (form $\frac{0}{0}$ )
$= lim k \to 0 {(1 + sin 2 k)}^{\frac{1}{k}}$
$= e^{lim k \to 0 \frac{1}{k} (sin 2 k)} = e^{2}$

|

Updated on:21/07/2023

Class 12 MATHS DEFINITE INTEGRAL

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-DEFINITE INTEGRATION -MATRIX MATCH_TYPE

Home
Ask Doubt
Profile