Let ∫∞0sinxxdx=α Then match the following lists and choose the correct code. :

Text Solution
The correct Answer is:4
I=∫∞0sin5xxdx
Let 5x=t
∴dx=15dt
∴I=∫∞0sin(t)t/5.dt5=∫∞0sinttdt=α
b. I=∫sin2x0dx
=∫∞0(sin2x)(1x2)dx
=[sin2x(−1x)]∞0−∫∞0(2sinxcosx)×(−1x)dx
=[−sin2xx]∞0+∫∞0sin2xxdx put 2x=t
=limx→∞[−sin2xx]−limx→∞[−sin2xx]+α
=0−0+α=α
c. I=∫∞0sin3xxdx
I=14[3∫∞0sinxxdx−∫∞0sin3xxdx]
=14[3α−α]=α2
d. ∫∞0sink1xcosk2xxdx
=12∫∞02sink1xcosk2xxdx
=12∫∞0sin(k1+k2)x+sin(k1−k2)xxdx
=12(α+α)=α
∴∫∞0sin(k1x).cosk2xxdx−α=0
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - DEFINITE INTEGRATION EXERCISE - NUMERICAL VALUE_TYPE28videos
DEFINITE INTEGRATION
- BOOK - CENGAGE PUBLICATIONCHAPTER - DEFINITE INTEGRATION EXERCISE - JEE MAIN12videos
DEFINITE INTEGRATION
- BOOK - CENGAGE PUBLICATIONCHAPTER - DEFINITE INTEGRATION EXERCISE - LC_TYPE31videos
DEFINITE INTEGRATION
- BOOK - CENGAGE PUBLICATIONCHAPTER - CURVE TRACINGEXERCISE - EXERCISES24videos
CURVE TRACING
- BOOK - CENGAGE PUBLICATIONCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer5videos
DETERMINANT
Similar Questions
Knowledge Check
- Question 1 - Select One
Match the following lists and then choose the correct code.
 AabcdqsrpBabcdpsrsCabcdqspsDabcdspqr
AabcdqsrpBabcdpsrsCabcdqspsDabcdspqr - Question 2 - Select One
Match the following lists and then choose the correct code.
 AabcdprsqBabcdrsqpCabcdrqspDabcdpqsr
AabcdprsqBabcdrsqpCabcdrqspDabcdpqsr - Question 3 - Select One
Match the following lists and and then choose the correct code.

 AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
AabcdprqqBabcdqprsCabcdspqrDabcdrsqp
Consider limx→∞(x3+x2+x+sinxx2+2cosx−asinx−bx+c)=4. Now, match the following lists and then choose the correct code.
 View Solution
View SolutionConsider limx→∞(x3+x2+x+sinxx2+2cosx−asinx−bx+c)=4. Now, match the following lists and then choose the correct code.
 View Solution
View SolutionMatch List I with List II and choose the correct code
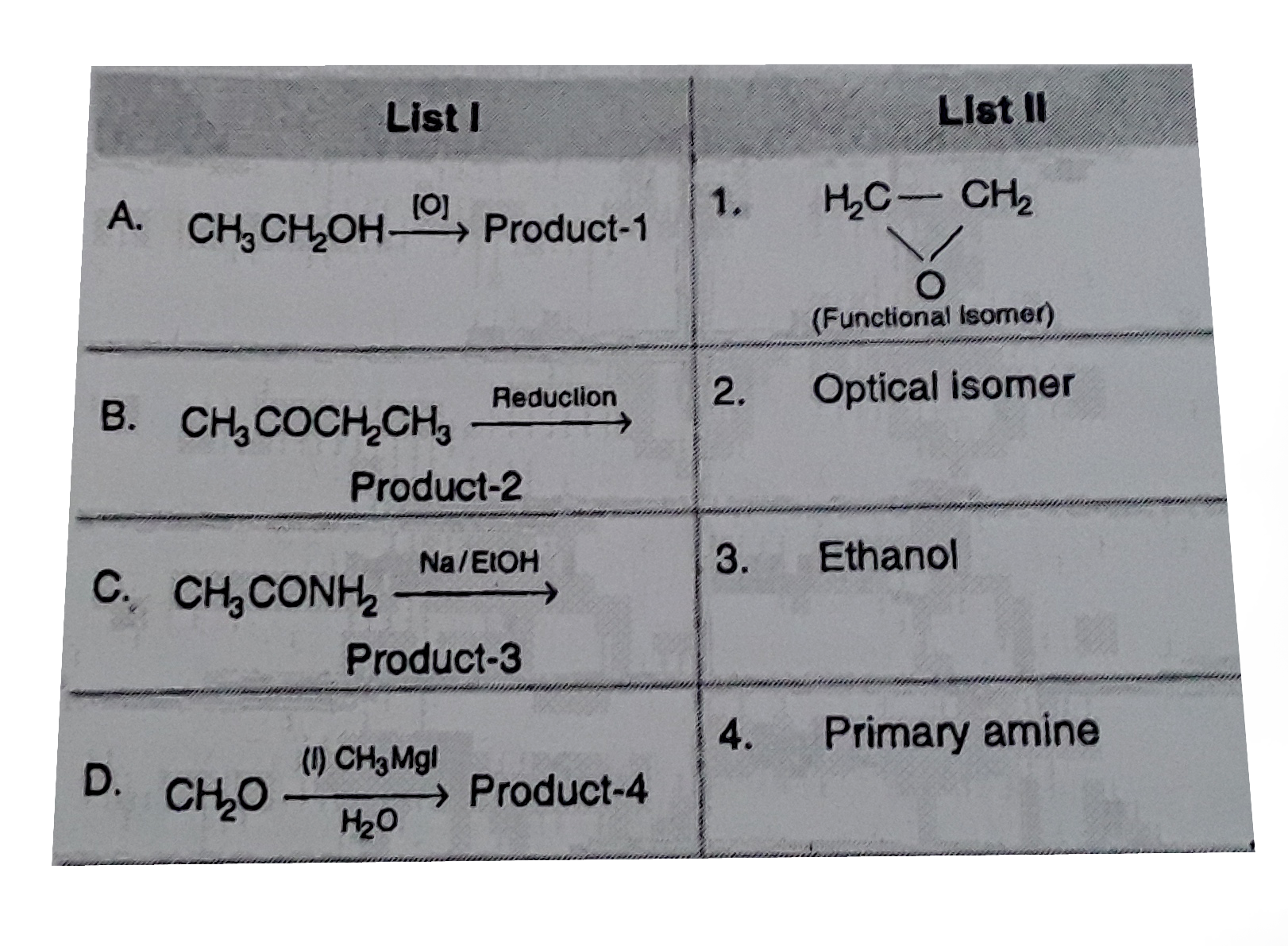 View Solution
View SolutionMatch the List-I with List-II and choose the correct answer from the codes:
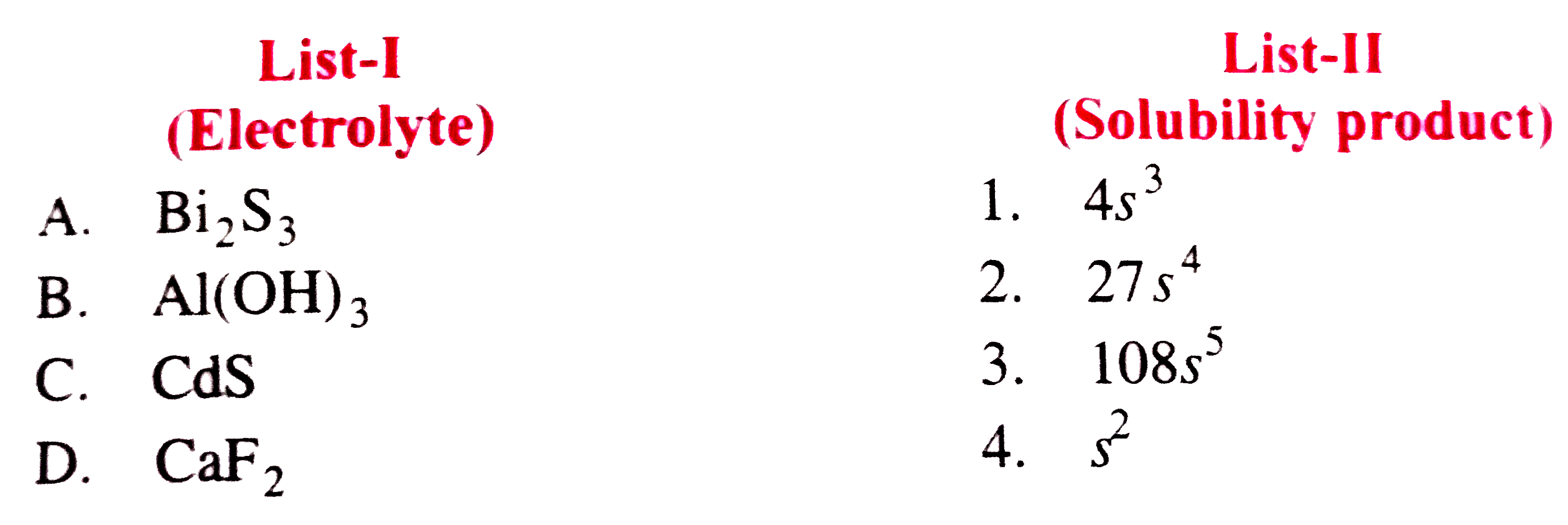 View Solution
View SolutionMatch the following two lists and choose the correct answer from the codes given below:
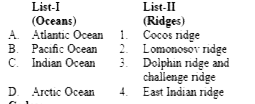 View Solution
View Solution

