A line L is a drawn from P(4,3) to meet the lines L−1andL2 given by 3x+4y+5=0 and 3x+4y+15=0 at points AandB , respectively. From A , a line perpendicular to L is drawn meeting the line L2 at A1. Similarly, from point B1. Thus, a parallelogram ∀1BB1 is formed. Then the equation of L so that the area of the parallelogram ∀1BB1 is the least is x−7y+17=0 7x+y+31=0 x−7y−17=0 x+7y−31=0Solution in Bengali
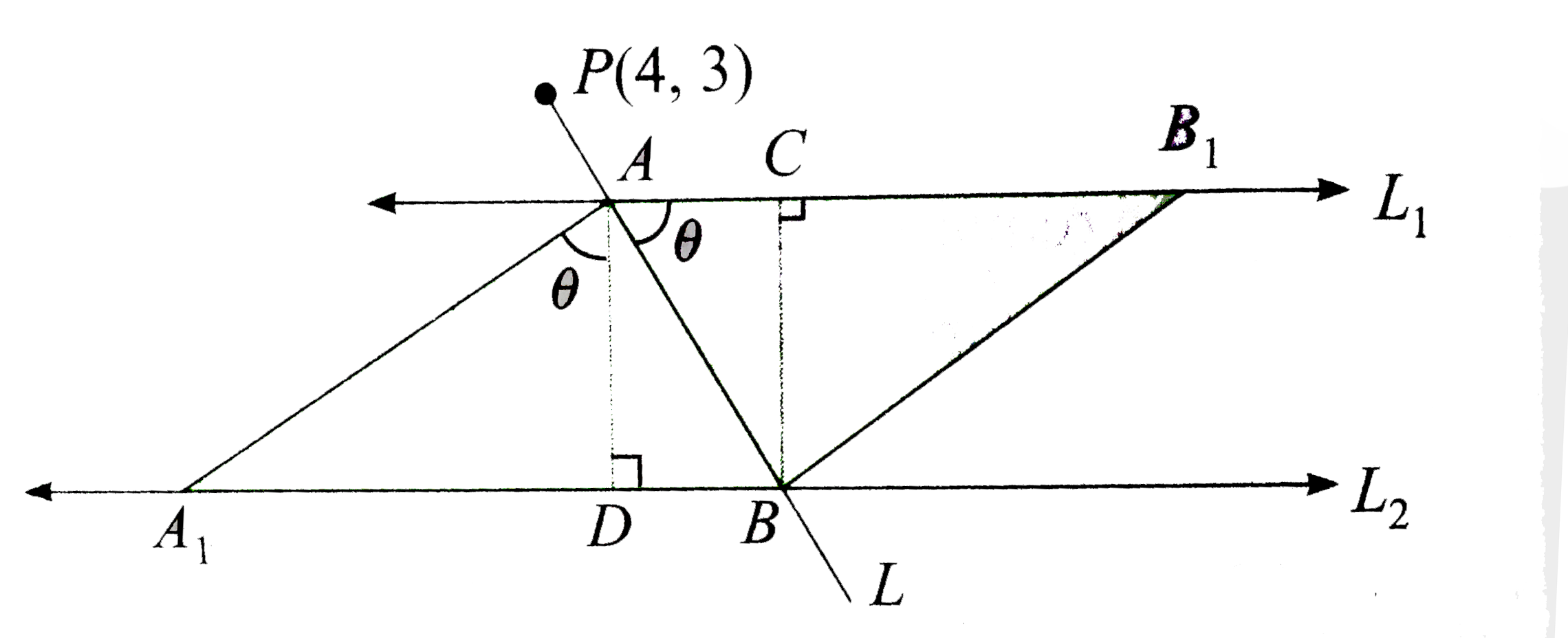
The given lines (L1 andL2) are parallel and the distance between them (BC or AD) is (15-5)/5 = 0 units. Let ∠BAC=θ. So, AB = BC cosec θ=2 cosec θ and AA1=AD sec θ=2 sec θ. Now, the area of parallelogram AA1BB1 is
Δ=AB×AA1=4sec θ cosecθ
=8sin2θ
Clearly,Δ is the least forθ=π/4. Let the slope of AB be m. Then,
tan45∘=∣∣∣m+3/41−(3m/4)∣∣∣
or 4m+3=±(4−3m)orm=17or−7
Hence, the equation of L is
x-7y+17=0
or 7x + y -31=0
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE12videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.123videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Show that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
05:11View SolutionFind the equation of the right bisector of the line segment joining the points (3,4) and (-1,2).
02:07View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
02:36View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
02:36View SolutionA line is a drawn from P(4,3) to meet the lines L1andl2 given by 3x+4y+5=0and3x+4y+15=0 at points AandB respectively. From A , a line perpendicular to L is drawn meeting the line L2 at A1 Similarly, from point B1 Thus a parallelogram ∀1BB1 is formed. Then the equation of L so that the area of the parallelogram ∀1BB1 is the least is (a) x−7y+17=0 (b) 7x+y+31=0 (c) x−7y−17=0 (d) x+7y−31=0
07:44View SolutionFind the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x−7y+5=0 and 3x+y=0.
02:58View Solutionरेखाओ x−7y+5=0 और 3x+y=0 के प्रतिच्छेद बिंदु से खींची गई और y - अक्ष के सामन्तर रेखा का समीकरण ज्ञात कीजिए ।
04:16View Solutionरेखाओं x-7y+5=0 और 3x+y = 0 के प्रतिच्छेद बिन्दु से खींची गई और Y- अक्ष के समान्तर रेखा का समीकरण ज्ञात कीजिए।
03:31View SolutionShow that the lines x−7y−22=0,3x+4y+9=0 and 7x+y−54=0 form a right angled isosceles triangle.
05:27View SolutionFind the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x−7y+5=0 and 3x+y=0.
03:38View SolutionFind the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x−7y+5=0 and 3x+y=0.
02:04View SolutionFind the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x−7y+5=0 and 3x+y=0.
05:39View SolutionA line is a drawn from P(4,3) to meet the lines L1andl2 given by 3x+4y+5=0and3x+4y+15=0 at points AandB respectively. From A , a line perpendicular to L is drawn meeting the line L2 at A1 Similarly, from point B1 Thus a parallelogram ∀1BB1 is formed. Then the equation of L so that the area of the parallelogram ∀1BB1 is the least is (a) x−7y+17=0 (b) 7x+y+31=0 (c) x−7y−17=0 (d) x+7y−31=0
03:19View SolutionFind the equation of the line parallel to y-axis and drawn through the point of intersection of the lines x−7y+5=0 and 3x+y=0.
03:16View SolutionFind the equation of the line parallel to Y -axis and drawn through the point of intersection of the lines x−7y+5=0and3x+y=0.
04:25View Solutionरेखाओ 4 x - 7y + 10 = 0, x + y = 5 तथा 7x + 4y = 15 द्वारा बनाए गए त्रिभुज का लम्बकेन्द्र है
07:05View Solution

