A regular polygon has two of its consecutive diagonals as the lines √3x+y−√3 and 2y=√3 . Point (1,c) is one of its vertices. Find the equation of the sides of the polygon and also find the coordinates of the vertices.Solution in Bengali
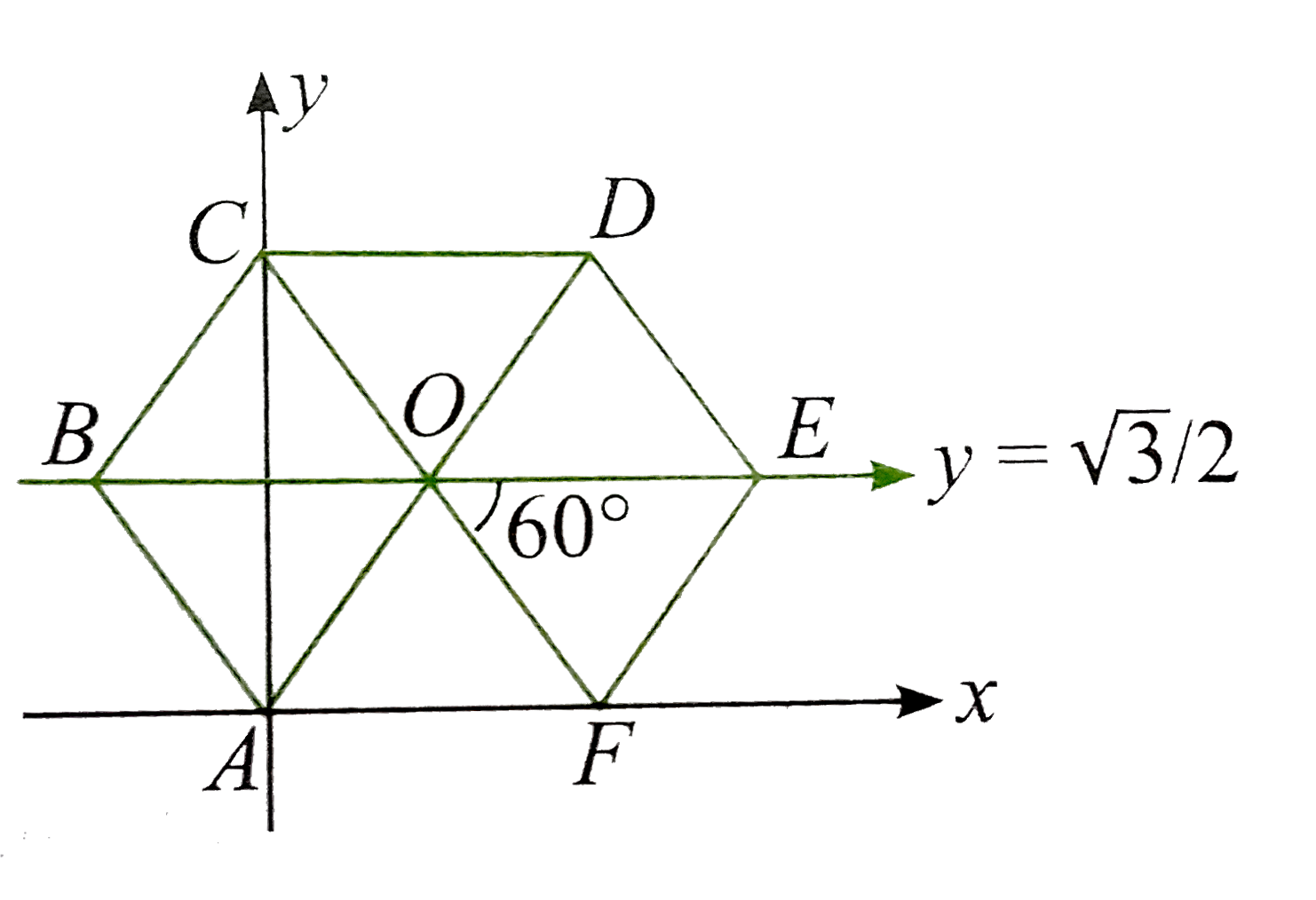
Two consecutive diagonals are the lines √3x=√3 and y=√3/2.
The angle between these two lines is 60∘. As the polygon is regular, it will be a hexagon.
The center of the polygon is (1/2,√3/2), and (1,0)lies on √3x+y=√3. Hence,
OF=
⎷(12−1)2+(√32)2=1
The equation of the third diagonal will be y =√3x. The coordinates of the vertices are as follows:
D(1,√3),A(0,0),C(0,√3),F(1,0),E(3/2,√3/2),B(−1/2,√3/2)
The equations of the sides are
←→AF≡y=0
←→CD≡y=√3
←→FE≡y=√3(x−1)
←→AB≡y=−√3x
←→BC≡y=√3(x+1)
←→ED≡y=−√3(x−2)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.24videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.37videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE12videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Two particles start from point (2, -1), one moving two units along the line x+ y = 1 and the other 5 units along the line x - 2y = 4, If the particle move towards increasing y, then their new positions are:
04:52View SolutionFind the points on y−ais whose perpendicular distance from the line 4x−3y−12=0 is 3.
10:38View SolutionShow that the lines 4x+y−9=0,x−2y+3=0,5x−y−6=0 make equal intercepts on any line of slope 2.
13:14View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
01:04View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
03:52View SolutionShow that the points (a,a),(−a,−a) and (−√3a,√3a) are the vertices of an equilateral triangle. Also, find its area.
11:38View SolutionA regular polygon of 10 sides is constructed. In how many way can 3 vertices be selected so that no two vertices are consecutive?
04:09View SolutionA regular polygon has two of its consecutive diagonals as the lines √3x+y−√3 and 2y=√3 . Point (1,c) is one of its vertices. Find the equation of the sides of the polygon and also find the coordinates of the vertices.
03:38View SolutionA regular polygon has 20 sides. Find the number of diagonals of the polygon.
02:42View SolutionIf the number of diagonals of a regular polygon is three times the number of its sides, find the number of sides of the polygon.
04:33View SolutionShow that the four lines y=0,y=2,y−√3x=0andy+√3x=8√3 form a cyclic trapezium . Find the coordinates of its vertices and also its area.
07:04View SolutionA(-3, 5) and B(1, 7) are two consecutive vertices of a parallelogram. If the point of intersection of its diagonals be (1, 1), then find its other two vertices.
07:37View SolutionA regular polygon of n sides is constructed. No. of ways 3 vertices be selected so that no two vertices are consecutive is
05:21View SolutionA regular polygon of 10 sides is constructed No. of ways 3 vertices be selected so that no two vertices are consecutive is
07:46View SolutionA regular polygon of 10 sides is constructed. In how many way can 3 vertices be selected so that no two vertices are consecutive?
02:47View SolutionThe coordinates of two consecutive vertices A and B of a regular hexagon ABCDEF are (1,0) and (2,0), respectively. The equation of the diagonal CE is (a)√3x+y=4 (b) x+√3y+4=0 (c)x+√3y=4 (d) none of these
03:56View Solution

