Question

Find the values of $\alpha$ such that the variable point $(\alpha ,\text{tan}\alpha )$ lies inside the triangle whose sides are
$y=x+\sqrt{3}-\frac{\pi }{3},x+y+\frac{1}{\sqrt{3}}+\frac{\pi }{6}=0\text{and}x-\frac{\pi }{2}=0$

Answer

`-(pi)/(6) lt alpha lt (pi)/(3)`

Explanation

Given lines are
`y = x+sqrt(3) -(pi)/(3) " " (1)`
`x+y+(1)/sqrt(3) +(pi)/(6) = 0 " " (2)`
`"and " x-(pi)/(2) = 0 " " (3)`
Variable point `(alpha, "tan" alpha)` lies on the curve y=tan x.
So, we draw the given lines and curve y=tan x.

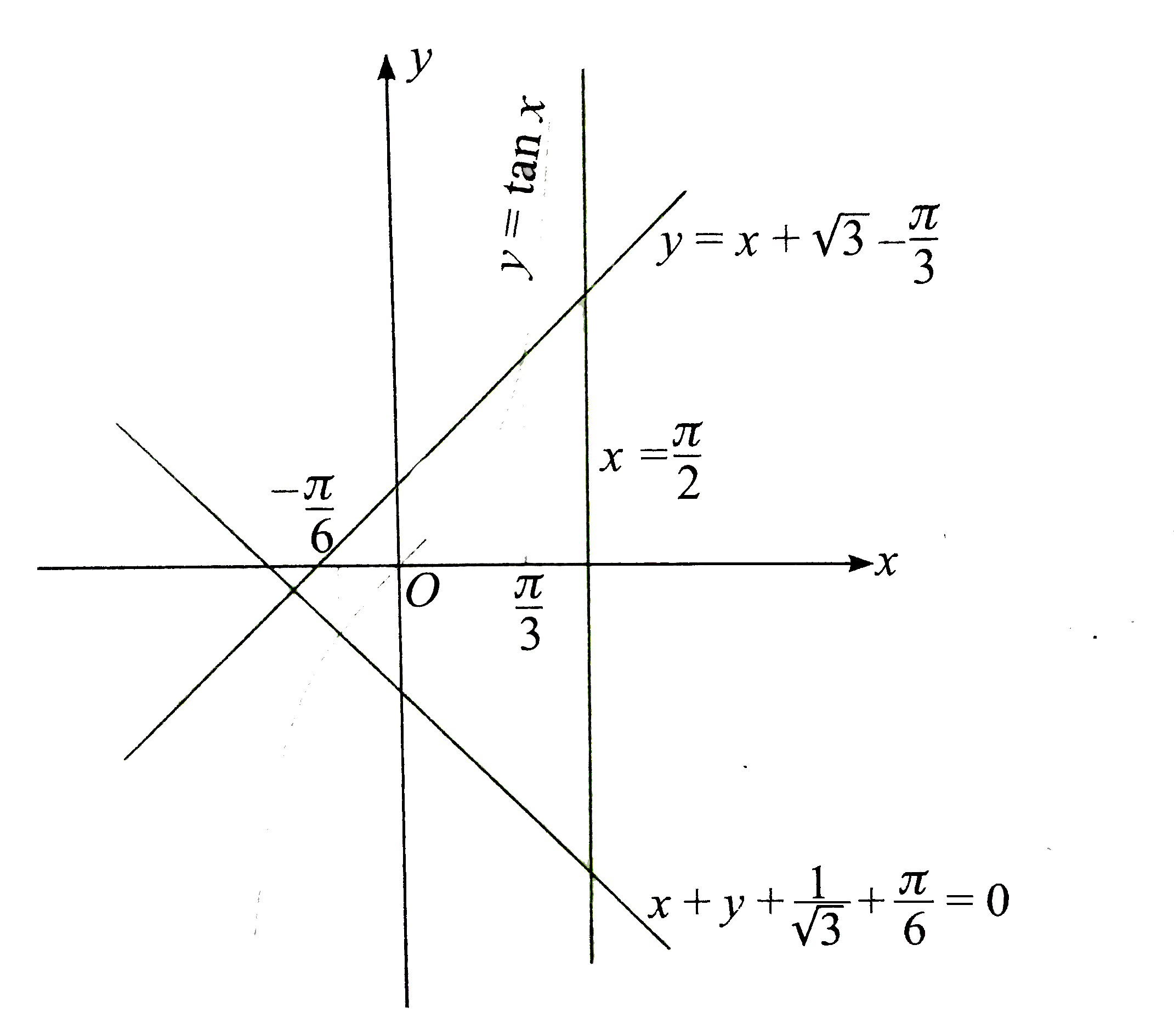
By hit and trial method, we find that line (1) cuts the curve.
`y="tan" x "for" x=(pi)/(3) " and line (2) cuts the curve for " x = -(pi)/(6).`
`"Hence, point "(alpha, "tan" alpha) " lies inside the triangle if" -(pi)/(6) lt alpha lt (pi)/(6).`