Find the area of the region in which points satisfy
3≤|x|+|y|≤5.Solution in Bengali
The correct Answer is:32 sq. units
We have 3≤|x|+|y|≤5.
|x|+|y|≤5 means that points lie inside the square endpoints of whose diagonal are (±5,0) and (0,±5).
|x|+|y|≥3 means that points lie outside the square endpoints of whose diagonal are (±3,0) and (0,±3).
So, common region is as shown in the figure.
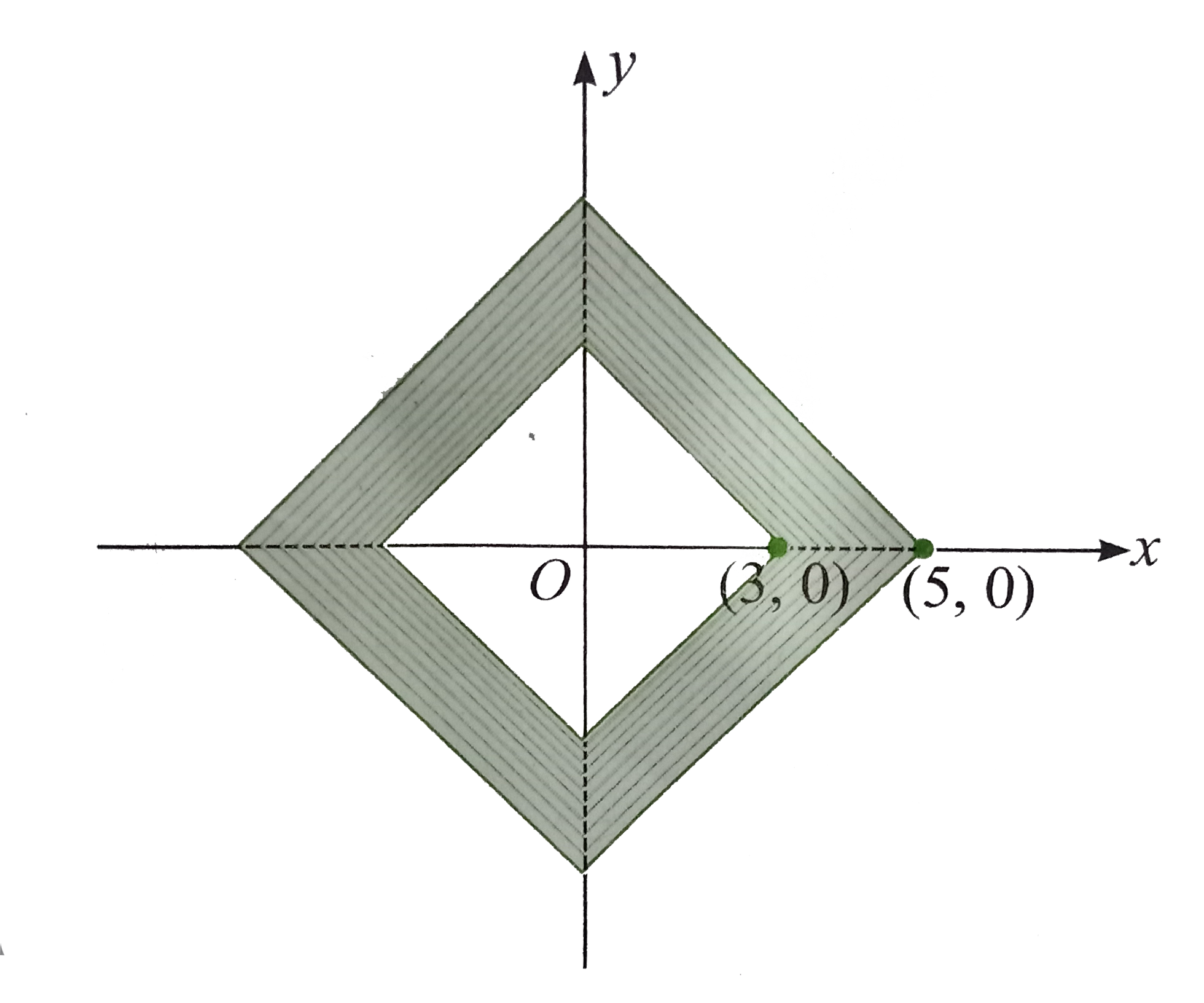
Area of region=4(12×5×5−12×3×3)=32sq.units
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.58videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.65videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.37videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Find the equation of the bisector of the obtuse angle between the lines 3x−4y+7=0 and 12x+5y−2=0.
08:47View SolutionIf aandb are two arbitrary constants, then prove that the straight line (a−2b)x+(a+3b)y+3a+4b=0 will pass through a fixed point. Find that point.
04:17View SolutionFind the points on y−ais whose perpendicular distance from the line 4x−3y−12=0 is 3.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
05:38View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
11:50View SolutionFind the area of the region formed by x2+y2−6x−4y+12≤0. y≤x and x≤52.
03:05View SolutionFind the area of region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}.
05:17View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
11:42View SolutionFind the area of the region in which points satisfy
3≤|x|+|y|≤5.06:22View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.13:01View SolutionFind the area of the region [x,y):x2+y2≤1≤x+y}
06:55View SolutionFind the area of the region {(x,y):0≤y≤x2,0≤y≤x+2,0≤x≤3}.
14:54View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
03:44View SolutionFind the area of the region in which points satisfy
3≤|x|+|y|≤5.05:47View SolutionFind the area of the region formed by the points satisfying
|x|+|y|+|x+y|≤2.04:01View SolutionFind the area bounded by the region given by : A={(x,y):x225+y29≤1≤x5+y3}.
03:42View Solution

