The straight line 3x+4y−12=0 meets the coordinate axes at AandB . An equilateral triangle ABC is constructed. The possible coordinates of vertex CSolution in Bengali
(2(1−3√34),32(1−4√3))
(−2(1+√3),32(1−√3))
(2(1+√3),32(1+√3))
(2(1+3√34),32(1+4√3))
The correct Answer is:A, D
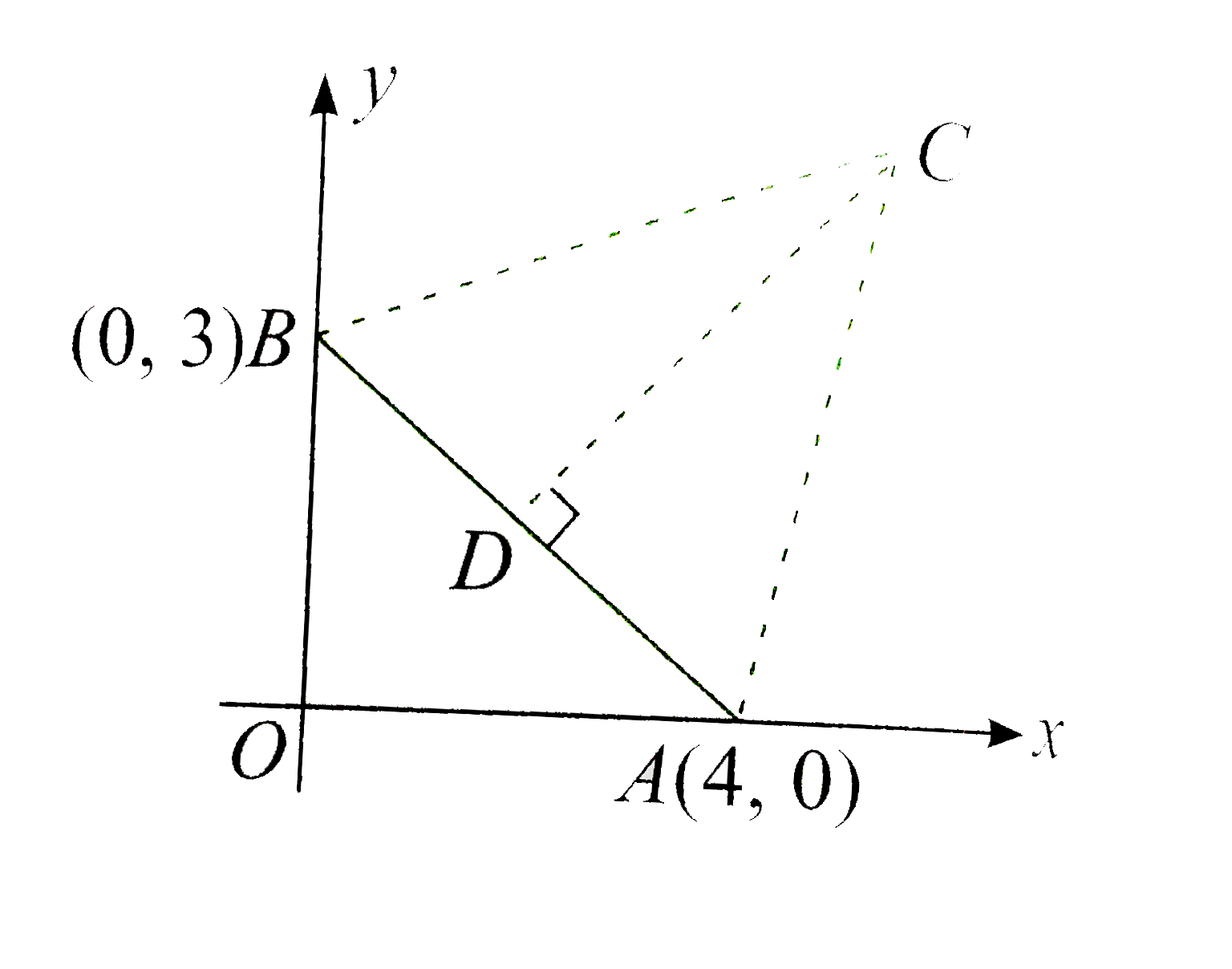
AB =5, D≡(2,32)
CD=5×√32=5√32
Slope of AB=−34
Slope of CD =34
If C≡(h,k),then
h−23/5=k−3/24/5=±5√32
or h=2(1−3√34),k=32(1−4√3)
or h=2(1+3√34),k=32(1+4√3)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)8videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (SINGLE CORRECT ANSWER TYPE)82videos
STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
Let l be the line belonging to the family of straight lines (a+2b)x+(a−3b)y+a−8b=0,a,b∈R, which is farthest from the point (2,2), then area enclosed by the line L and the coordinate axes is
04:35View SolutionMatch the following lists:
 03:21View Solution
03:21View SolutionFind the equations of the diagonals of the square formed by the lines x=o,y=0,x=1andy=1.
05:07View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
05:58View SolutionThe number of distinct real roots of x4−4x3+12x2+x−1=0is_____.
01:54View SolutionThe straight line 3x+4y−12=0 meets the coordinate axes at AandB . An equilateral triangle ABC is constructed. The possible coordinates of vertex C (a) (2(1−3√34),32(1−4√3)) (b)(−2(1+√3),32(1−√3)) (c)(2(1+√3),32(1+√3)) (d)(2(1+3√34),32(1+4√3))
02:38View SolutionThe incentre of the triangle formed by the line 3x+4y-12=0 with the coordinate axis is
06:44View SolutionIn Fig.,delta ABC is an equilateral triangle with coordinates of B and C as B(1,0) and C(5,0) . Find the coordinates of vertex A
05:17View SolutionThe line 3x+4y=12 cuts x -axis at A and y_(-) axis at B. The equation of the excircle of the triangle formed by this line and coordinate axes,opposite to the vertex B is
06:07View SolutionThe area (in square unit) of the triangle which the straight line 3x+4y-12=0 forms with the coordinate axes is -
01:48View SolutionThe line 3x+4y-12=0 meets the coordinate axes at A and B. find the equation of the circle drawn on AB as diameter.
07:00View SolutionThe straight line 3x+4y−12=0 meets the coordinate axes at AandB . An equilateral triangle ABC is constructed. The possible coordinates of vertex C (a) (2(1−3√34),32(1−4√3)) (b)(−2(1+√3),32(1−√3)) (c)(2(1+√3),32(1+√3)) (d)(2(1+3√34),32(1+4√3))
08:04View SolutionTriangle ABC with AB=13,BC=5, and AC=12 slides on the coordinates axes with AandB on the positive x-axis and positive y-axis respectively. The locus of vertex C is a line 12x−ky=0. Then the value of k is_____________
08:03View SolutionA straight line passing through P(3,1) meets the coordinate axes at AandB . It is given that the distance of this straight line from the origin O is maximum. The area of triangle OAB is equal to
04:12View SolutionFind the area of the triangle formed by the line 3x−4y+12=0 with the coordinate axes.
07:00View Solution

