Consider point P(x, y) in first quadrant. Its reflection about x-axis is Q(x1,y1). So, x1=x and y1=−y.
This may be written as : {x1=1.x+0.yy1=0.x+(−1)y
This system of equations can be put in the matrix as :
[x1y1]=[100−1][xy]
Here, matrix [100−1] is the matrix of reflection about x-axis. Then find the matrix of reflection about the line y=x.
Solution in Bengali
(i) Reflection of (x, y) about y-axis is (x1,y1)≡(−x,y).
∴x1=(−1)x+0y
and y1=0x+y
∴[x1y1]=[−1001][xy]
(ii) Reflection of (x, y) about the line y=x is (x1,y1)≡(y,x).
∴x1=0x+y
y1=x+0y
∴[x1y1]=[0110][xy]
(iii) Reflection of (x, y) about origin is (x1,y1)≡(−x,−y).
∴x1=−x+0y
y1=0x−y
∴[x1y1]=[−100−1][xy]
(iv) Reflecton in line t=xtanθ or (sinθ)x−(cosθ)y=0:
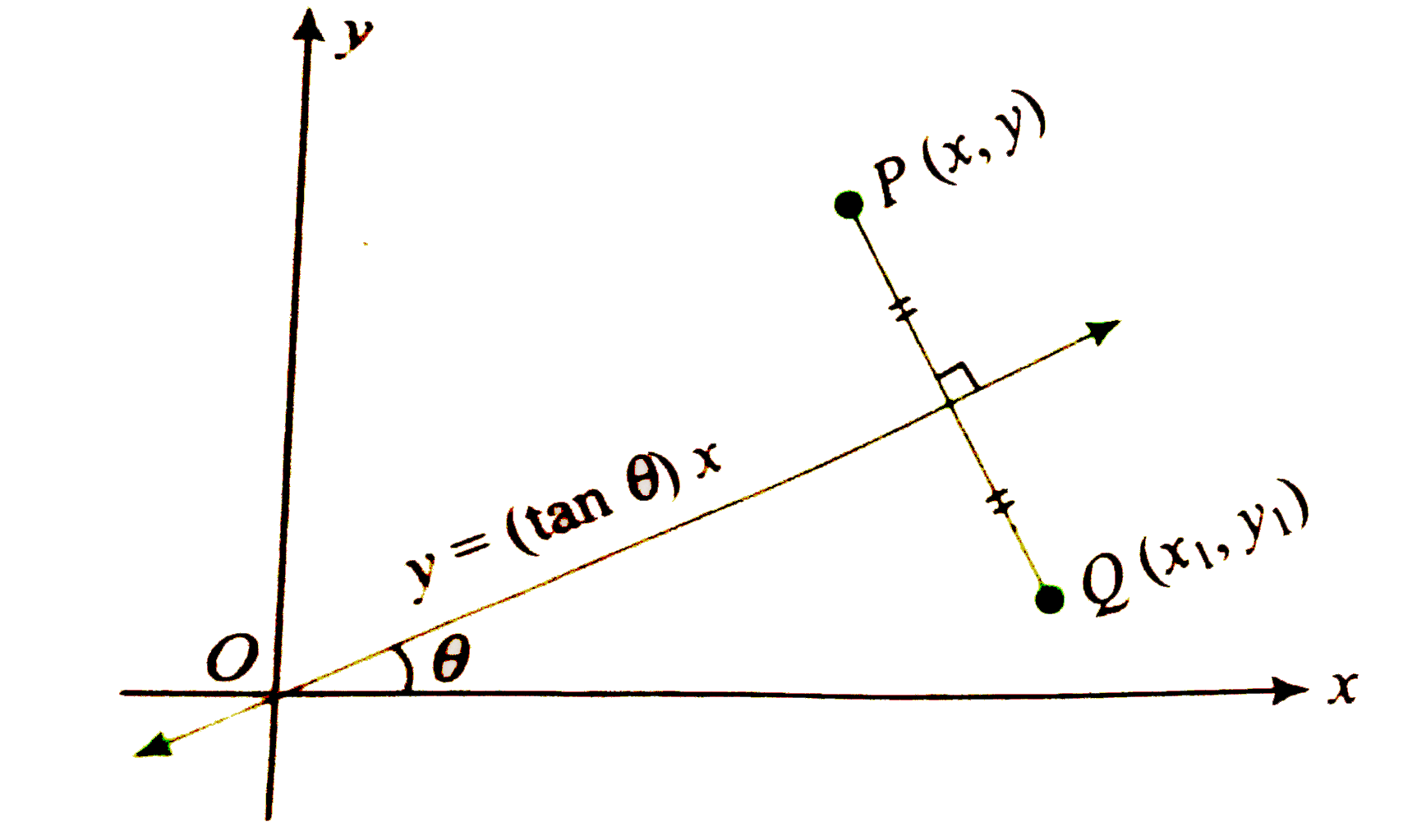
We kanow that
x1−xsinθ=y1−y−cosθ=−2((sinθ)x−(cosθ)y)sin2θ+cos2θ
∴x1=(1−2sin2θ)x+(2sinθcosθ)y
or x1=(cos2θ)x+(sin2θ)y
y1=(2sinθcosθ)x+(1−2cos2θ)y
or y1=(sin2θ)x−(cos2θ)y
Thus, [x1y1]=[cos2θsin2θsin2θ−cos2θ][xy]
By putting θ=0,π/2,π/4, we can get the reflection matrices x-axis, y-axis and the line y=x, respectively.
Topper's Solved these Questions
Similar Questions
Statements -1 : ~(p↔~q) is equivalent to p↔q
Statement-2: ~(p↔~q) is a tautology.View SolutionIf y=cos−1√√1+x2+12√1+x2,thendydxisequa<o 12(1+x2),x∈R (b) 12(1+x2),x>0 −12(1+x2),x<0 (d) 12(1+x2),x<0
03:49View SolutionConsider point P(x, y) in first quadrant. Its reflection about x-axis is Q(x1,y1). So, x1=x and y(1)=−y.
This may be written as : {x1=1.x+0.yy1=0.x+(−1)y
This system of equations can be put in the matrix as :
[x1y1]=[100−1][xy]
Here, matrix [100−1] is the matrix of reflection about x-axis. Then find the matrix of
(i) reflection about y-axis
(ii) reflection about the line y=x
(iii) reflection about origin
(iv) reflection about line y=(tanθ)xView SolutionPoint P(x, y) is rotated by an angle θ in anticlockwise direction. The new position of point P is Q(x1,y1). If [x1y1]=A[xy], then find matrix A.
08:03View Solutionमान लीजिए ΔABC के शीर्ष A(x1,(y1),B(x2,y2) तथा C(x3,y3) है तथा ΔABC का क्षेत्रफल =1/2|Δ|
जहाँ , Δ=∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣
यदि P(x,y) इस प्रकार हो , कि ∣∣ ∣ ∣∣xy1x1y11x2y21∣∣ ∣ ∣∣+∣∣ ∣ ∣∣xy1x1y11x3y31∣∣ ∣ ∣∣=0 हो ,
तो A तथा P से जाने वाली रेखा02:23View SolutionIf the tangent at (x0,y0) to the curve x3+y3=a3 meets the curve again at (x1,y1), then x1x0+y1y0 is equal to
01:33View Solutionसमीकरण (x−x1)(x−x2)+(y−y1)(y−y2)=0 से निरूपित वृत्त का व्यास ज्ञात कीजिए।
05:42View SolutionCentre of the circle
(x−x1)(x−x2)+(y−y1)(y−y2)=0 is07:50View SolutionThe point whose coordinates are x=x1+t(x2−x1),y=y1+t(y2−y1) divides the join of (x, y) and (x2,y2) in the ratio
02:20View Solutionउस बिन्दु का बिन्दुपथ ज्ञात कीजिए जो बिन्दुओं (x1,y1) और (x2,y2) संरेख होंगे। इसलिए,
y2−y1x2−x1=y−y1x−x1.02:09View SolutionA : The reflection of (6, 8) in the line x=y is (8, 6)
R : The reflection of (x1,y1) in the line x=y is (y1,x1)03:05View SolutionTabular |[x, y, 1], [x_(1), y_(1), 1], [x_(2), y_(2), 1]| = 0 Denotes
04:49View SolutionConsider point P(x, y) in first quadrant. Its reflection about x-axis is Q(x1,y1). So, x1=x and y(1)=−y.
This may be written as : {x1=1.x+0.yy1=0.x+(−1)y
This system of equations can be put in the matrix as :
[x1y1]=[100−1][xy]
Here, matrix [100−1] is the matrix of reflection about x-axis. Then find the matrix of reflection about the line y=x.
08:18View SolutionPoint P(x, y) is rotated by an angle θ in anticlockwise direction. The new position of point P is Q(x1,y1). If [x1y1]=A[xy], then find matrix A.
02:57View SolutionIf the tangent at (x0,y0) to the curve x3+y3=a3 meet the curve again at (x1y1) prove that x1x0+y1y0=−1
09:38View SolutionThe equation of line whose midpoint (x1,y1) is in between the axes, is.............. A) xx1+yy1=2 B) xx1+yy2=12 C) xx1+yy2=12
D) None of these09:32View Solution

