Evaluate: [(lim)x→0tan−1xx], where [.]represent the greatest integer functionSolution in Bengali
See the graphs of y=x and tan−1x in the following figure.
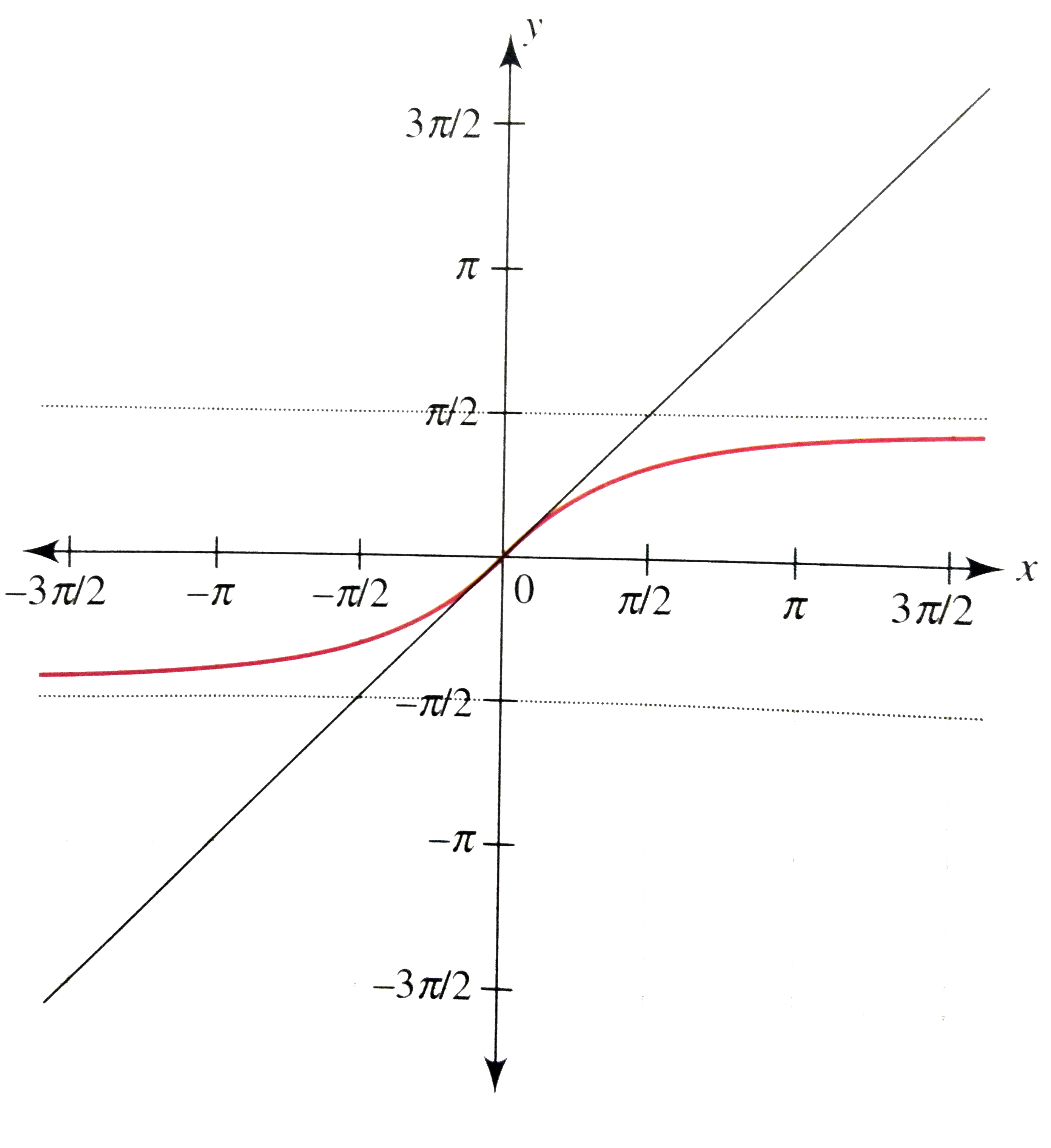
For f(x)=tan−1(x)=11+x2
∴ f'(0)=1
So the curve touches the line y = x at x = 0
For x>0,f'(x)<1
So the graph of y=tan−1x lies below the graph of y = x.
From the graph, when x→o+, the graph of y = x is above the graph of y=tan−1x
or tan−1x<x⇒tan−1xx<1⇒[limx→0+tanxx]=0
Thus [limx→0+tanxx]=0
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercises 1.181videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION78videos
GRAPHICAL TRANSFORMATIONS
Similar Questions
Draw the graph of y=tan−1x−cot−1x.
06:53View SolutionFollowing is the graph of y = f'(x) and f(0) = 0 .
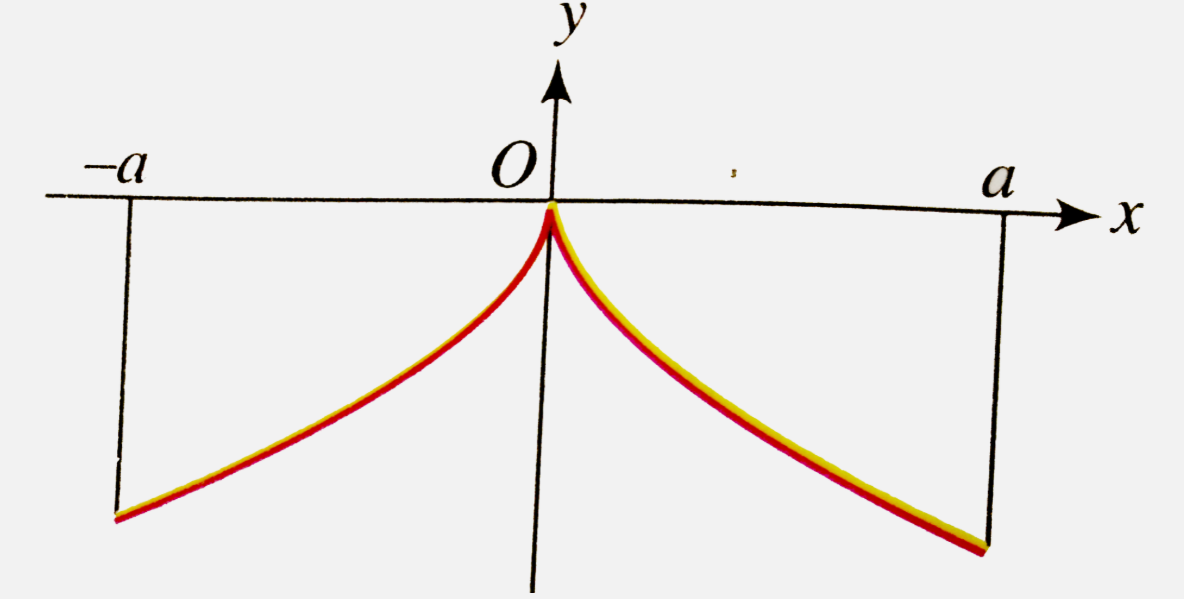
(a) What type of function y = f'(x) is ? Odd or even?
(b) What type of function y = f(x) is ? Odd or even?
(c) What is the value of ∫a−af(x)dx?
(d) Has y = f(x) point of inflection?
(e) What is the nature of y = f(x)? Monotonic or non-monotonic?05:55View SolutionPlot y=|x|,y+x−2∣,andy=|x|2∣
05:14View SolutionFind x satisfying [tan−1x]+[cot−1x]=2, where [.] represents the greatest integer function.
02:50View SolutionEvaluate: [(lim)x→0tan−1xx], where [.]represent the greatest integer function
01:57View SolutionEvaluate: (lim)x→0tanxx where [.] represents the greatest integer function
03:56View SolutionEvaluate : (lim)x→2+ [x−2]log(x−2) , where [.] represents the greatest integer function.
07:06View Solution(lim)x→0[sin−1xtan−1x]= (where [.] denotes the greatest integer function) a. 0 b. 1 c. -1 d. none of these
02:49View SolutionIf f(x)=x(e|x|+[x]−2|x|+[x]) then (where [.] represents the greatest integer function) (lim)x→0+f(x)=−1 b. (lim)x→0−f(x)=0 c. (lim)x→0□f(x)=−1 d. (lim)x→0□f(x)=0
03:17View SolutionFind x satisfying [tan−1x]+[cot−1x]=2, where [.] represents the greatest integer function.
04:07View SolutionEvaluate: (lim)x→0sinxx,where[.] represents the greatest integer function.
03:53View SolutionEvaluate: [(lim)x→0tan−1xx], where [.]represent the greatest integer function
01:50View SolutionEvaluate: (lim)x→0tanxx where [.] represents the greatest integer function
06:02View SolutionGiven (lim)x→0f(x)x2=2,where [.] denotes the greatest integer function, then (A) (lim)x→0[f(x)]=0 (B) (lim)x→0[f(x)]=1 (C)(lim)x→0[f(x)x] does not exist (D)(lim)x→0[f(x)x] exists
10:47View SolutionIf f(x)=x(e|x|+[x]−2|x|+[x]) then (where [.] represents the greatest integer function) (lim)x→0+f(x)=−1 b. (lim)x→0−f(x)=0 c. (lim)x→0□f(x)=−1 d. (lim)x→0□f(x)=0
01:48View SolutionFind x satisfying [tan−1x]+[cos−1x]=2, where [] represents the greatest integer function.
02:43View Solution

