Find tan−1.x√a2−x2 in terms of sin−1, where x∈(0,a)Solution in Bengali
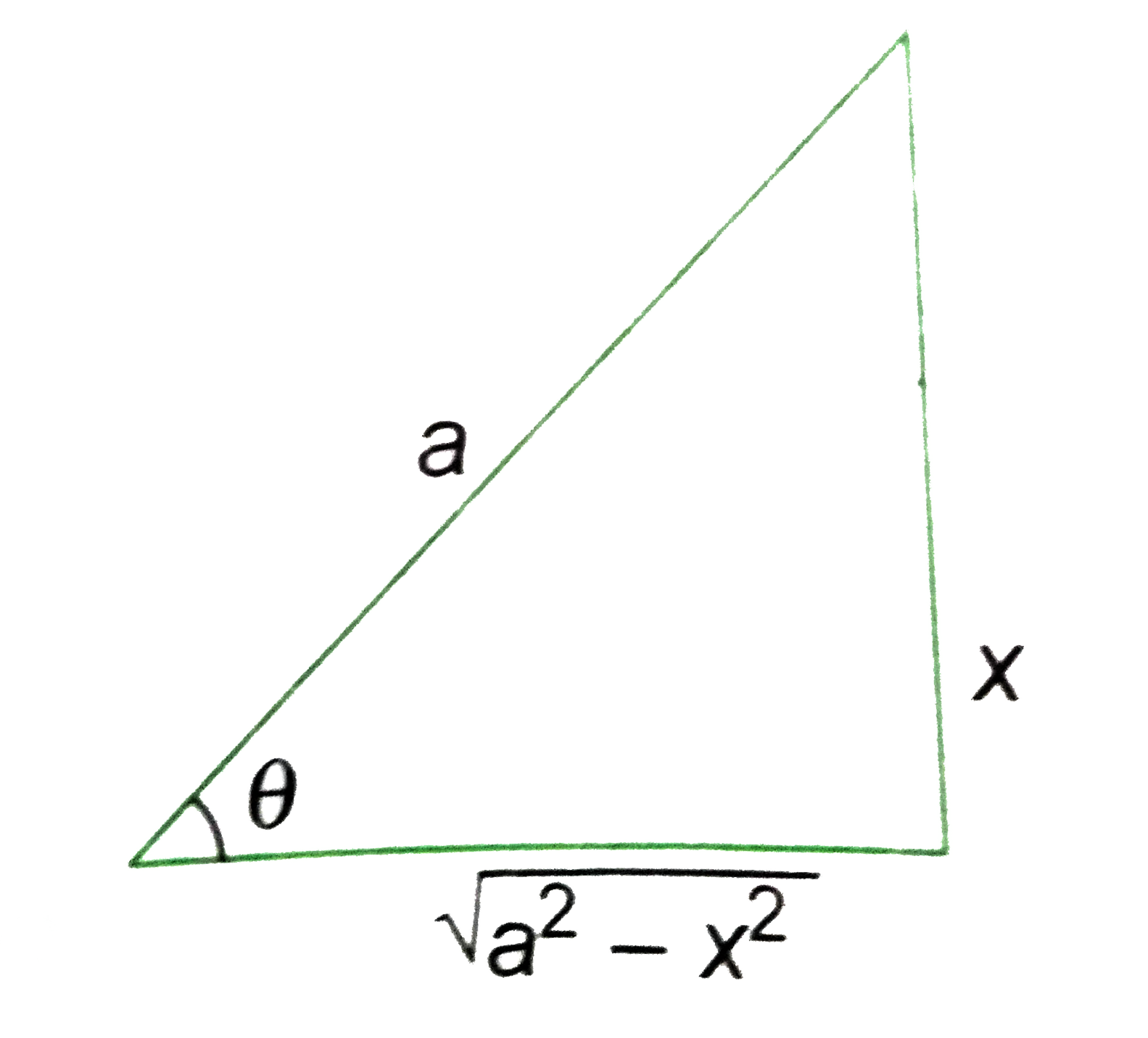
We have tan−1(x)√a2−x2=θ
From the triangle,
tan−1(x)√a2−x2=sin−1(x)a
Topper's Solved these Questions
Similar Questions
The points with position vectors →x+→y,→x−→yand→x+λ→y are collinear for all real values of λ.
00:56View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
03:47View SolutionFind tan−1x√a2−x2 in terms of sin−1 where x∈(0,a).
06:14View SolutionF i n ddydxify=tan−1(√1+x2−1x), where x≠0
03:32View Solutiony=tan−1(√1+x2+√1−x2√1+x2−√1−x2),where −1<x<1,x≠0
02:11View Solutionif x greater than equal to 0 and less than equal to 1/2 then find the value of tan[sin^(-1){(x)/(sqrt(2))+sqrt((1-x^(2))/(2))}-sin^(-1)x]
02:28View SolutionExpress sin−1x in terms of (i) cos−1√1−x2 (ii) tan−1x√1−x2 (iii) cot−1√1−x2x
05:37View SolutionFind tan−1.x√a2−x2 in terms of sin−1, where x∈(0,a)
01:47View SolutionIf y=tan−1[√1+sinx−√1−sinx√1+sinx+√1−sinx] where 0<x<π2 find dydx
04:17View SolutionFind tan−1x√a2−x2 in terms of sin−1 where x∈(0,a).
03:44View SolutionFind tan−1.x√a2−x2 in terms of sin−1, where x∈(0,a)
08:20View SolutionFinddydxify=tan−1(√1+x2−1x), where x≠0
06:45View SolutionDifferentiate w.r.t x : tan−1{√1+sinx+√1−sinx√1+sinx−√1−sinx},0<x<π2
02:26View SolutionFind the derivative of tan−1√1+x2−1x with respect to tan−1(2x√1−x2)1−2x2 at x = 0
02:18View SolutionExpress sin−1x in terms of (i) cos−1√1−x2 (ii) tan−1x√1−x2 (iii) cot−1√1−x2x
02:50View SolutionFind tan−1x√a2−x2 in terms of sin−1 where x∈(0,a).
03:44View Solution

