Convert the following Cartesian coordinates to the corresponding polar coordinates using positive r and negative r. (i) (ii)(iii)((iv)(v)−1,1(vi))(vii) (viii) (ii) (ix)(x)((xi)(ξi)2,−3(xiii))(xiv) (xv)Solution in Bengali
(i) For the second quadrant point (x,y)≡(−1,1), we have
tanθ=yx=−1⇒θ=3π4
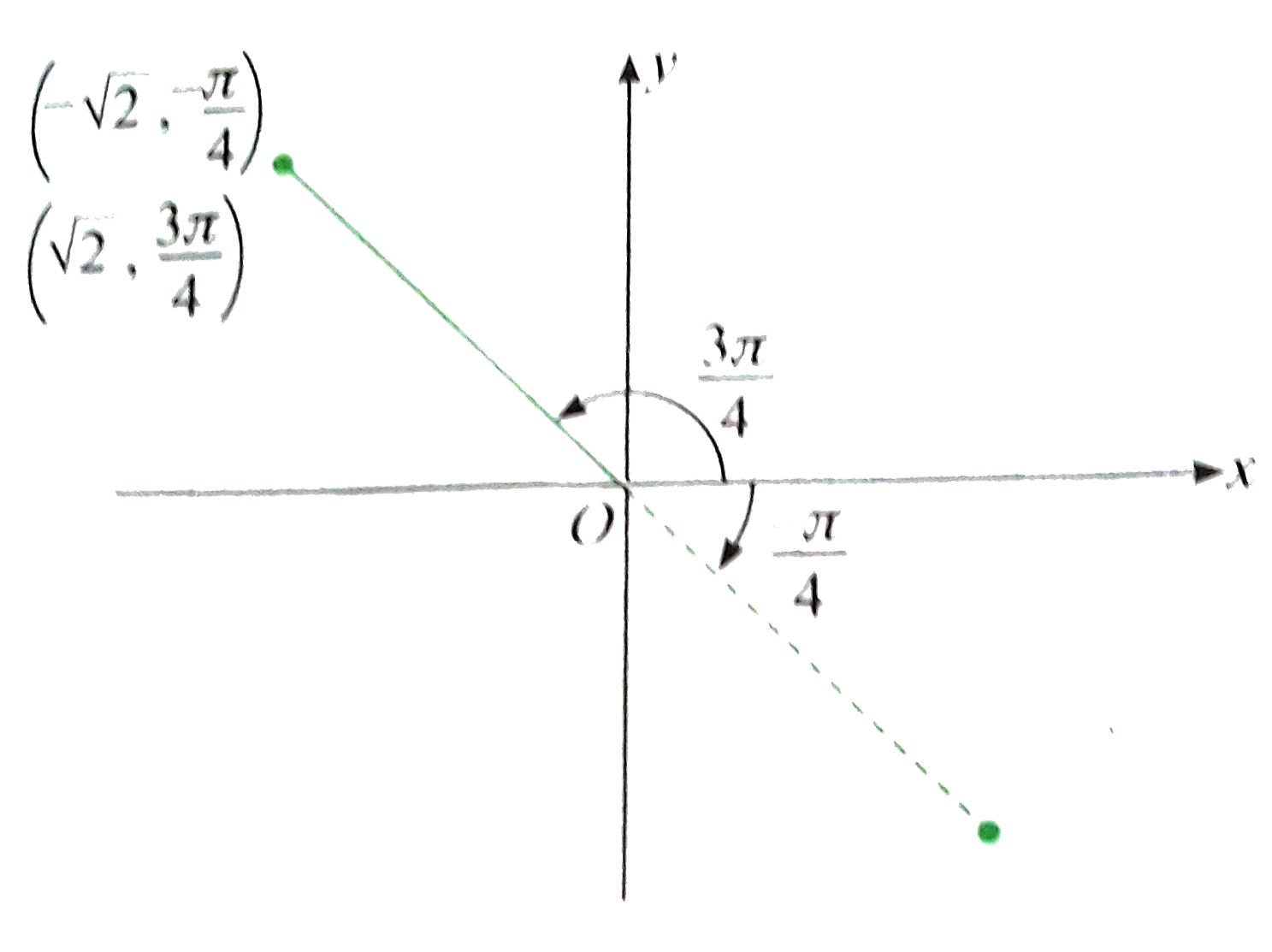
Using positive r, we have
r=√x2+y2=√(−1)2+(1)2=√2
So, one set of polar coordinates is (r,θ)≡(√2,3π/4)
Using negative r, we have coordinates =(−√2,−π/4)
(ii) For the fourth quadrant point (x,y)≡(2,−2), we have
tanθ=−32
⇒θ=tan−1(−32)=−tan−1^32
Using positive r, we have
r=√x2+y2=√(−3)2+(2)2=√13
So, one set of polar coordinates is
(r,θ)≡(√13,−tan−132)
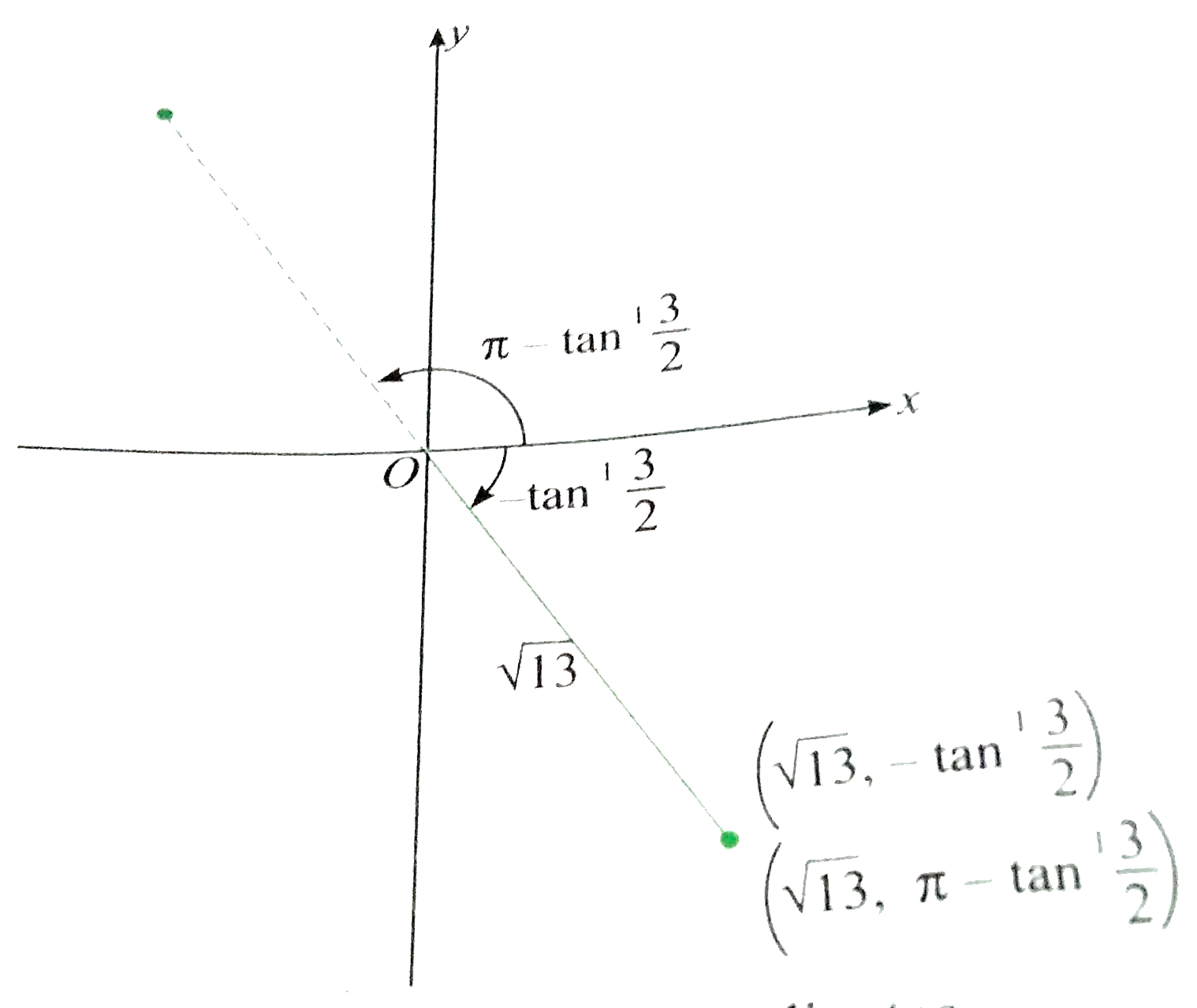
Using negative r, we have coordinates
=(−√13,π−tan−132)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.531videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.541videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.511videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Convert y=10 into a polar equation.
05:42View SolutionExpress the polar equation r−2cosθ in rectangular coordinates.
04:40View SolutionConvert the following points from polar coordinates to the corresponding Cartesian coordinates.
(2,π/3)03:13View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
01:30View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
03:12View SolutionConversion of coordinates in Polar conversion form:(i) Convert the following Cartesian coordinates to the corresponding polar coordinates using positive r and negative r . (i)(-1;1) (ii) (2;-3)
13:31View SolutionWrite the following in Hindu Arabic numerals: (i)DCXCVII (ii) KCIX (iii) KKKCDVI (iv)C K X X I (V) X IDCC(vi)DXII
09:56View SolutionIn Fig.23, OA and OB are opposite rays: (i) If (ii)(iii)x=(iv)(v)25(vi)0(vii)(viii),(ix) (x) what is the value of (xi)(ξi)y?(ξii) (xiv) (xv) If (xvi)(xvii)y=(xviii)(ξx)35(xx)0(xxi)(xxii),(×iii) (xxiv) what is the value of (xxv)(×vi)x?(×vii) (xxviii)
10:20View SolutionIn Fig.78, we have (i) (ii)(iii)∠MLY=2∠LMQ,(iv) (v) find (vi)(vii)∠LMQ(viii) (ix) (x) (xi)(ξi)∠XLM=(xiii)(ξv)((xv)(xvi)2x−10(xvii))(xviii)0(xix)(xx)(×i) (xxii) and (xxiii)(×iv)∠LMQ=x+(xxv)(×vi)30(xxvii)0(xxviii)(xxix),(×x) (xxxi) find (xxxii)(×ξii)x.xxxiv (xxxv) (xxxvi) (xxxvii)(×xviii)∠XLM=∠PML, (xxxix) (xl) find (xli)(xlii)∠ALY(xliii) (xliv) (xlv) (xlvi)(xlvii)∠ALY=(xlviii)(xlix)((l)(li)2x−15(lii))(liii)0(liv)(lv), ∠LMQ=(lvi)(lvii)((lviii)(lix)x+40(lx))(lxi)0(lxii)(lxiii),(lξv) (lxv) find (lxvi)(lxvii)x.lxviii (lxix)
13:06View SolutionFind the values of xandy: (i) x+3i=6−9iy (ii) (x+iy)−(3−2i)=5+i (iii) i=x+2yi (iv) 4x+i(x−y)=2−5i (v) (x+2iy)(2−i)2=10(1−i)
08:51View SolutionFind the real values of x and y for which :
(i)(1−i)x+(1+i)y=1−3i(ii)(x+iy)(3−2i)=(12+5i)(iii)x+4yi=ix+y+3(iv)(1+i)y2+(6+i)=(2+i)x(v)(x+3i)(2+iy)=(1−i)(vi)(1+i)x−2i(3+i)+(2−3i)y+i(3−i)=i04:25View Solution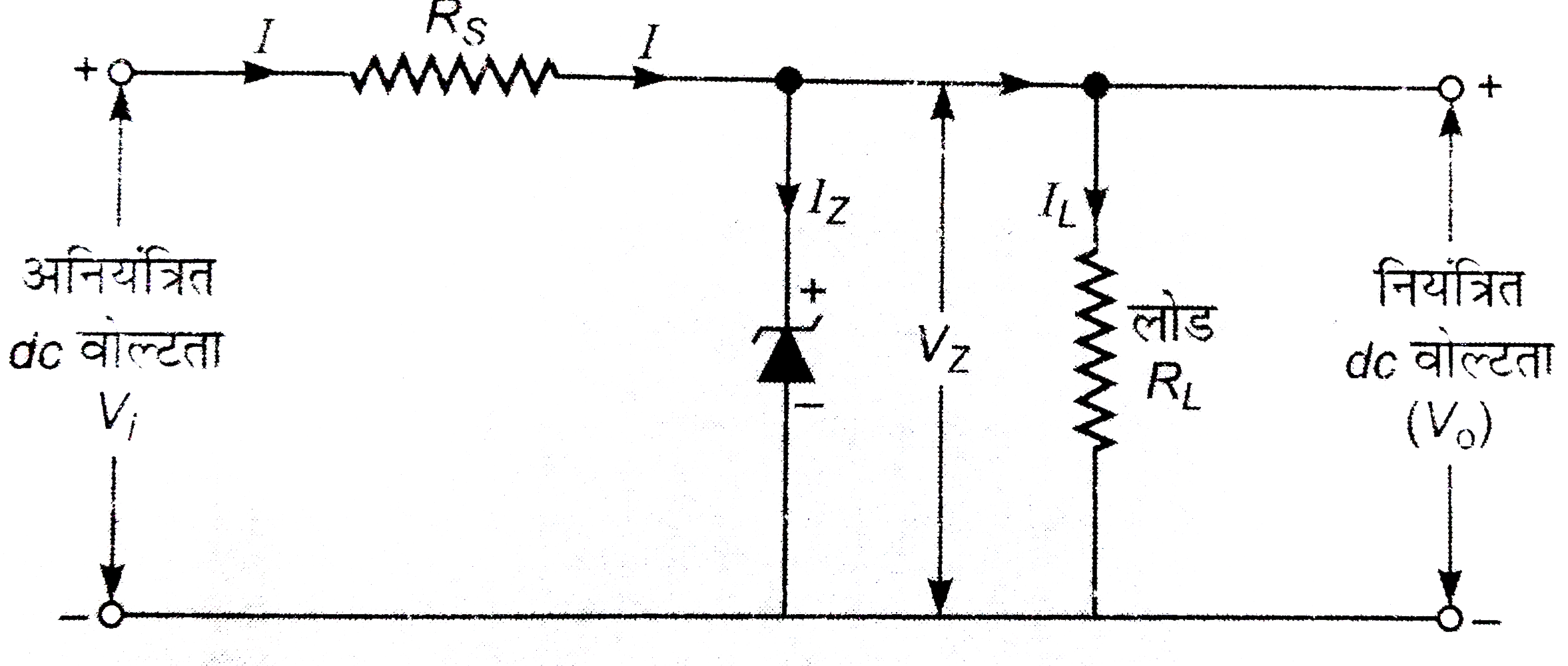
चित्र में RS=500 ओम , VZ=10V तथा RL=1kΩ हैं। परिपथ में IZ,IL तथा Vo का मान क्या होगा यदि -
(i ) Vi=30V है, (ii ) Vi=15V है, (iii ) Vi=5V है ?04:08View Solutionनिम्नलिखित में x और y के मान ज्ञात कीजिए-
(i) x+3i=6−9iy (ii) (x+iy)−(3−2i)=5+i
(iii) i=x+2yi (iv) 4x+i(x−y)=2−5i
(v) (x+2iy)(2−i)2=10(1−i)04:18View Solutionनिम्न के मान ज्ञात कीजिए :
(i)i28(ii)i58(iii)i19(iv)i−28(v)i−37(vi)−i−58(vii)i−19(viii)(−i)37(ix)(−i)−19(x)i+1i(xi)i10+i15(xii)i3+i2+i+203:59View SolutionSimplify the following :
(i) i7 (ii)i1729 (iii)i−1924+i2018 (iv)102∑n=1in (v)ii2i3…..i4002:53View SolutionEvaluate the following
(i) i9
(ii) i342
(iii) i998
(iv) i−63
(v) (i3+1i3)05:45View Solution

