Let $A B C D$ be a rectangle and $P$ be any point in its plane. Show that $A P^{2} + P C^{2} = P B^{2} + P D^{2} .$ Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is:NA

Let $A \equiv (0, 0), B \equiv (a, 0), C \equiv (a, b) and D \equiv (0, b)$
Let point P be (h,k).

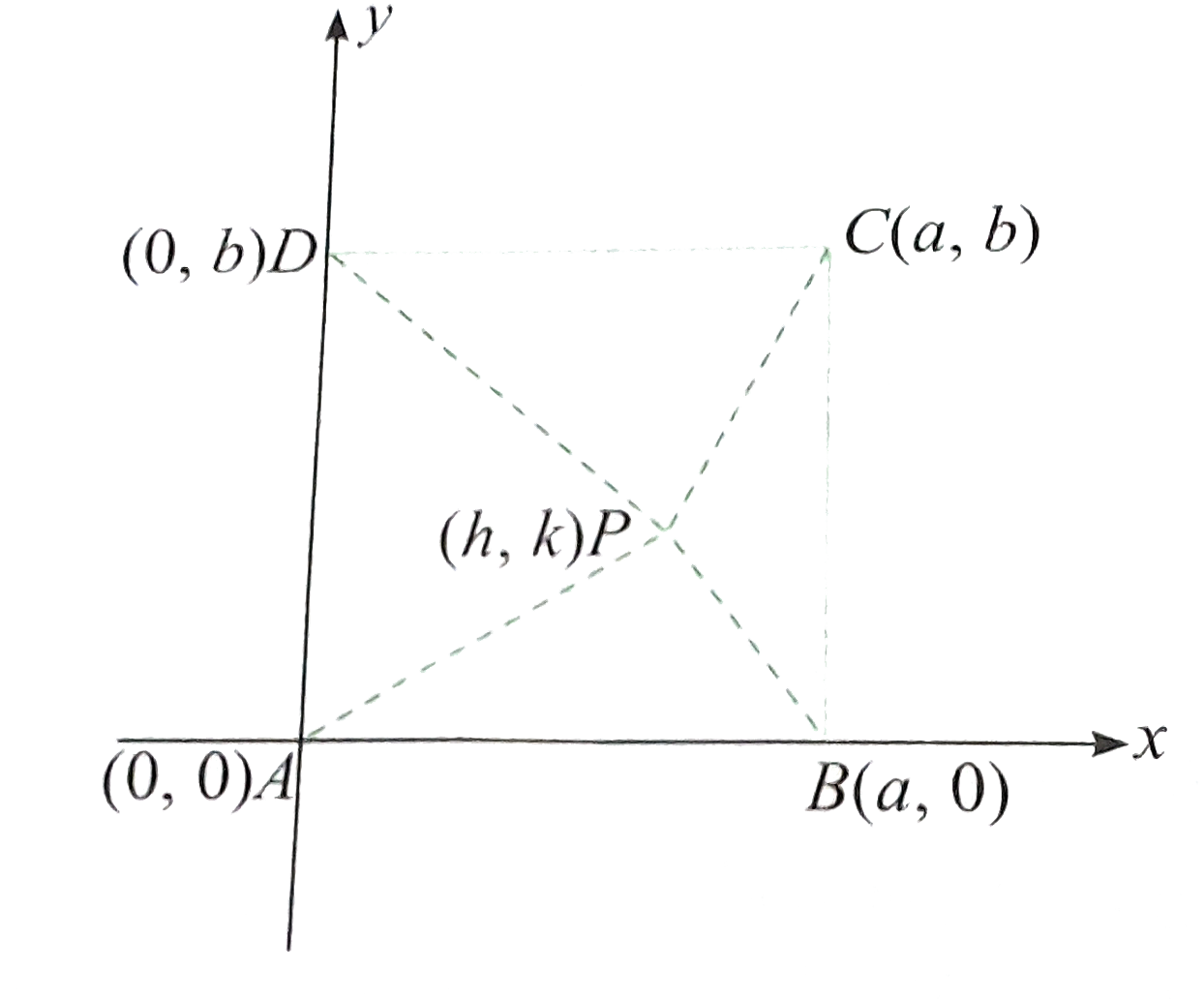
$∴ P A^{2} + P C^{2} = {(h - 0)}^{2} + {(k - 0)}^{2} + {(h - a)}^{2} + {(k - b)}^{2} = 2 h^{2} + 2 k^{2} - 2 k^{2} - 2 a h - 2 b k + a^{2} + b^{2}$
Also, $P B^{2} + P D^{2} = {(h - a)}^{2} + {(k - 0)}^{2} + {(h - 0)}^{2} + {(k - b)}^{2} = 2 h^{2} + 2 k^{2} - 2 a h - 2 b k + a^{2} + b^{2}$
Thus, $P A^{2} + P C^{2} = P B^{2} + P D^{2}$

|

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-COORDINATE SYSYEM -Concept applications 1.2

Home
Ask Doubt
Profile