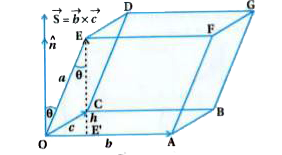
Find the volume of a parallelopiped having three coterminus vectors of equal magnitude $| \to a |$ and equal inclination $θ$ with each other.Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is: ${| \to a |}^{3} \sqrt{1 + 2 cos θ} (1 - cos θ)$

Let $\to a, \to b and \to c$ be three vectors of magnitude $| \to a |$ and equal inclination $θ$ with each other.
volume of parallelepiped = $(\to a . (\to b \times \to c) = [\to a \to b \to c]$
$and {[\to a \to b \to c]}^{2} = ∣ ∣ ∣ ∣ ∣ \begin{matrix} \to a . \to a & \to a . \to b & \to a . \to c \to b . \to a & \to b . \to b & \to b . \to c \to a . \to c & \to b . \to c & \to c . \to c \end{matrix} ∣ ∣ ∣ ∣ ∣$
${| \to a |}^{2} ∣ ∣ ∣ ∣ \begin{matrix} 1 & cos θ & cos θ cos θ & 1 & cos θ cos θ & cos θ & 1 \end{matrix} ∣ ∣ ∣ ∣$
${| \to a |}^{6} (2 {cos}^{3} θ - 3 {cos}^{2} θ + 1)$
${| \to a |}^{6} {(1 - cos θ)}^{2} (1 + 2 cos θ a)$
$or [\to a \to b \to c] = {| \to a |}^{3} \sqrt{1 + 2 cos θ} (1 - cos θ)$

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS -Exercises

Home
Ask Doubt
Profile