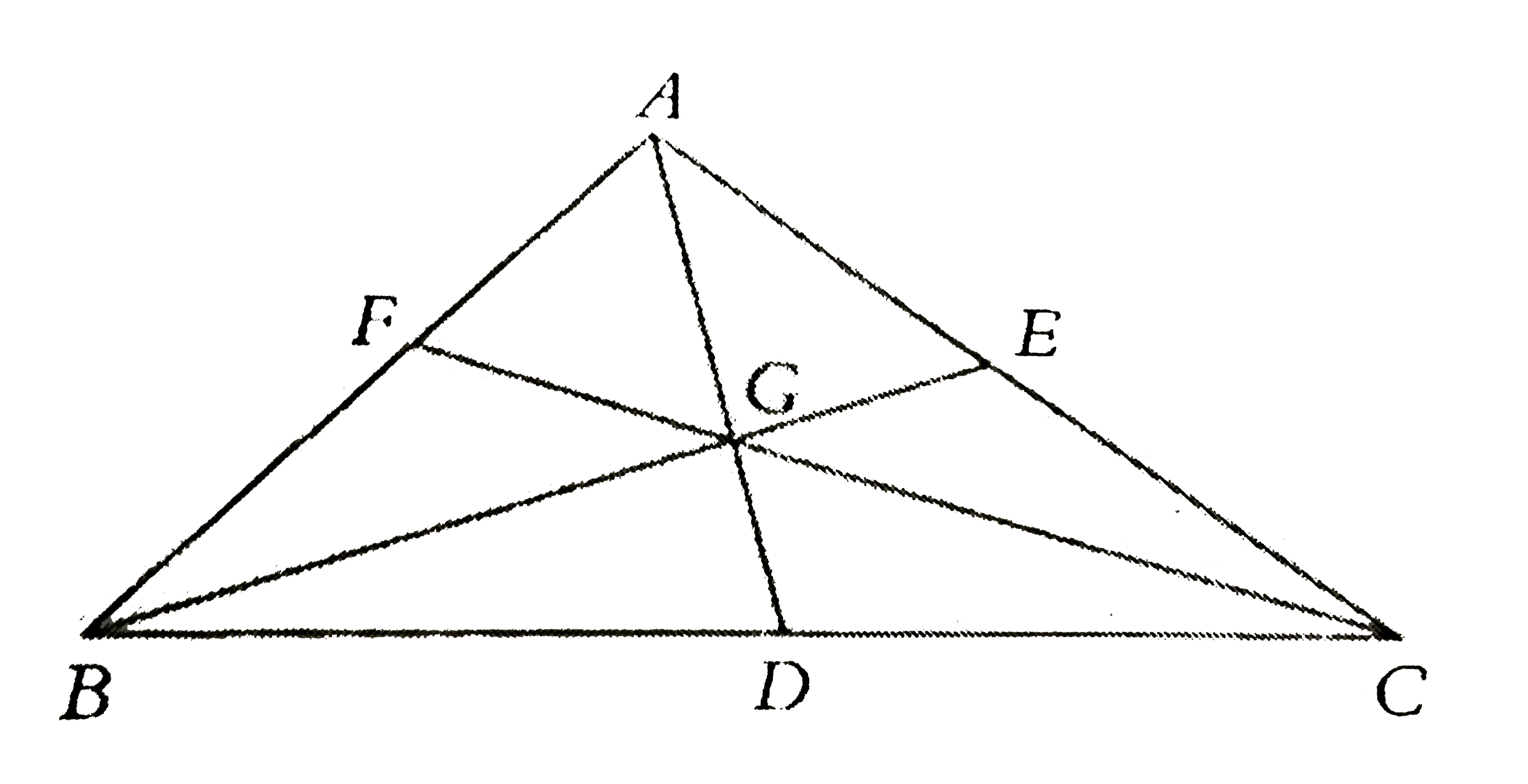
AD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2Solution in Bengali
Points A, F, G and E are concylic,

⇒BG.BE=BF.BA
⇒23(BE)2=12c2
⇒23×14(2a2+2c2−b2)=12c2 (Using Apollonius Theorem)
⇒2a2=b2+c2
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.108videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.114videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.87videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )8videos
PROGRESSION AND SERIES
- BOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions1119videos
RELATIONS AND FUNCTIONS
Similar Questions
In ΔABC, if r1<r2<r3, then find the order of lengths of the sides
12:50View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
View SolutionIf the incircle of the triangle ABC passes through its circumcenter, then find the value of 4sin.A2sin.B2sin.C2
02:25View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________03:08View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
06:00View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
02:04View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The height of the altitude drawn from point A is (in units)03:36View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
03:02View SolutionIn the given ΔABC,¯¯¯¯¯¯AD,¯¯¯¯¯¯BE and ¯¯¯¯¯¯CF are the medians. G is centroid. What is the ratio of the area of ΔBGD and ΔGCE?
 03:25View Solution
03:25View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are the points E(3,4) and F(1,2) respectively. The centroid of ΔABC ,G(3,2). equation of side AB is
03:14View SolutionA=(1,3,-2) is a vertex of triangle ABC whose centroid is G=(-1,4,2) then length of median through A is
04:37View SolutionThe three medians AD, BE and CF of ΔABC intersect at point G. If the area of ΔABC is 60 sq.cm. then the area of the quadrilateral BDGF is :
02:36View SolutionLet ABC be an acute- angled triangle and AD, BE, and CF be its medians, where E and F are at (3,4) and (1,2) respectively. The centroid of ΔABC G(3,2).
The coordinates of point D is ____________02:17View SolutionAD, BE and CF are the medians of triangle ABC whose centroid is G. If the points A, F, G and E are concyclic, then prove that 2a2=b2+c2
03:26View SolutionIn a ΔABC, G is centroid and AD, BE, CF are medians. Find the area of quadrilateral BDGF, if the area of ΔABC=72cm2
04:23View Solution

