If H is the orthocentre of triangle ABC, R = circumradius and P=AH+BH+CH, then (a) P=2(R+r) (b) max. of P is 3R (c) min. of P is 3R (d) P=2(R−r)Solution in Bengali
P=2(R+r)
max. of P is 3R
min. of P is 3R
P=2(R−r)
The correct Answer is:A, B
AH=2RcosA,BH=2RcosB,CH=2RcosC
∴P=2R(cosA+cosB+cosC)
=2R(1+rR)
=2(R+r)
We know that in any triangle, r≤R2
∴P≤2R+R
⇒P≤3R
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Matrix match type6videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercises80videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )8videos
PROGRESSION AND SERIES
- BOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions1119videos
RELATIONS AND FUNCTIONS
Similar Questions
Given that Δ=6,r1=2,r2=3,r3=6
Circumradius R is equal to a) 2.5 b)3.5 c)1.5 d)none of these02:58View Solutionshow that tan−1(12)+tan−1(211)=tan−1(34)
05:16View SolutionIn ΔABC,sinA(a−bcosC)sinC(c−bcosA)=
04:47View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________07:37View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
View SolutionIf (x+2) is a common factor of (px^(2)+qx+r) and (qx^(2)+px+r) then a p=q or p+q+r=0 b p=r or p+q+r=0 c) q=r or p+q+r=0 d p=q=-(1)/(2)r
02:17View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
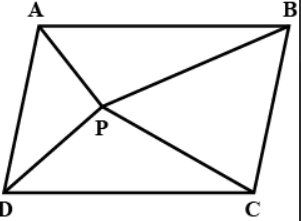 06:22View Solution
06:22View SolutionIf p,q, rare any real numbers,then (A) max(p,q)
07:33View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)
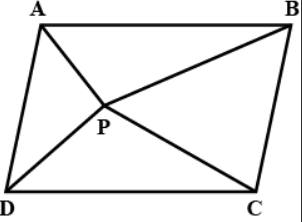 04:20View Solution
04:20View SolutionIf H is the orthocentre of triangle ABC, R = circumradius and P=AH+BH+CH, then
02:41View SolutionIf H is the orthocentre of the triangle ABC, R = circumradius and P=AH+BH+CH, then
09:21View SolutionIn a ΔABC, if p,q,r are the distances from the orthocentre to the vertices A,B,C respectively, then a q r + b r p+ c p q =
09:19View SolutionIf H is the orthocentre of triangle ABC,R= circumradius andP=AH+BH+CH , then (a) P=2(R+r) (b) maxofPis3R (c) minofPis3R (d) P=2(R−r)
08:34View SolutionIf p, q, r are any real numbers, then (A) max(p,q)<max(p,q,r) (B) min(p,q)=12(p+q−|p−q|)(C) max(p,q)<min(p,q,r) (D) None of these
03:44View SolutionIf H is the orthocentre of triangle ABC, R = circumradius and P=AH+BH+CH, then
01:57View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
05:35View Solution

