If D,E and F are the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF isSolution in Bengali
a zero vector
0
a unit vector
none of these
The correct Answer is:A, B
Let D, E and F be the mid-point of the sides of ΔABC.
E and F are mid-point of AC and AB, respectively
So, EF∣∣BCandEF=12BC
Thus, AD will also divide EF into equal parts.
Hence, DH is also median of ΔDEF
Similarly BE, median of ΔABC, is also median of ΔDEF.
These two lines meet at G.So the centroids of both triangles are same.
The orthocenter, O of ΔDEF is the point of intersection of the perpendiculars DH and EK drawn from D and E, respectively.
Since, EF∣∣BC, DH is perpendicular to BC also.
Similarly EK is perpendicular to AC.
So, orthocenter of ΔDEF and circumcentre of ΔABC is the same points
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Matrix match type6videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercises80videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )8videos
PROGRESSION AND SERIES
- BOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions1119videos
RELATIONS AND FUNCTIONS
Similar Questions
Given that Δ=6,r1=2,r2=3,r3=6
Circumradius R is equal to a) 2.5 b)3.5 c)1.5 d)none of these09:44View Solutionshow that tan−1(12)+tan−1(211)=tan−1(34)
03:47View SolutionIn ΔABC,sinA(a−bcosC)sinC(c−bcosA)=
02:36View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________05:24View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
04:56View SolutionIn the given figure, a circle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14 cm, BC = 8 cm and CA = 12 cm. Find the lengths AD, BE and CF.
06:10View SolutionIf D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
05:28View SolutionABC एक समबाहु त्रिभुज है AB , BC CA भुजाओं पर क्रम्स: D , E और F मध्य बिंदु लिए गए है ताकि AD =BE -CF होगा तुह AE BF , CD द्वारा निर्मित त्रिभुज होगा कैसा होगा
View SolutionIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OA10:18View SolutionThe incircle of ΔABC touches the sides AB, BC and CA of the triangle at the points D, E and F. Prove that AD+BE+CF=AF+CE+BD=12 (The perimeter of ΔABC)
04:49View Solutionयदि ΔABCकी भुजाओं BC,CA और AB के मध्यबिंदु क्रमशः D,E और F हों तो सिद्ध कीजिए कि AD रेखाखंड EF को समद्विभाजित करती है।
02:28View SolutionIf D, E, F are the mid-points of the sides BC, CA and AB respectively of △ABC, then ¯¯¯¯¯¯AD+23¯¯¯¯¯¯BE+13¯¯¯¯¯¯CF=
05:55View SolutionLet D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
04:02View SolutionIn ΔABC the midpoints are D,E and F of the sides AB,BC and CA, then ΔDEF:ΔABC is
04:04View SolutionIn ΔABC and ΔDEF, AB= DE, AB || DE, BC= EF and BC|E|F. Vertices A, B and C are joined to vertices D, E and F respectively. Show that
AD|C|F and AD = CF
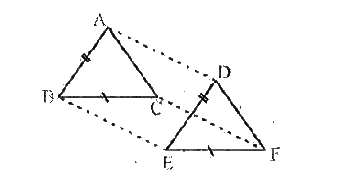05:19View SolutionD, E and F are the mid-points of the sides of BC, CA and AB of the ΔABC. If ΔABC=16Sq.cm., then the area of the trapezium FBCE is-
03:07View Solution