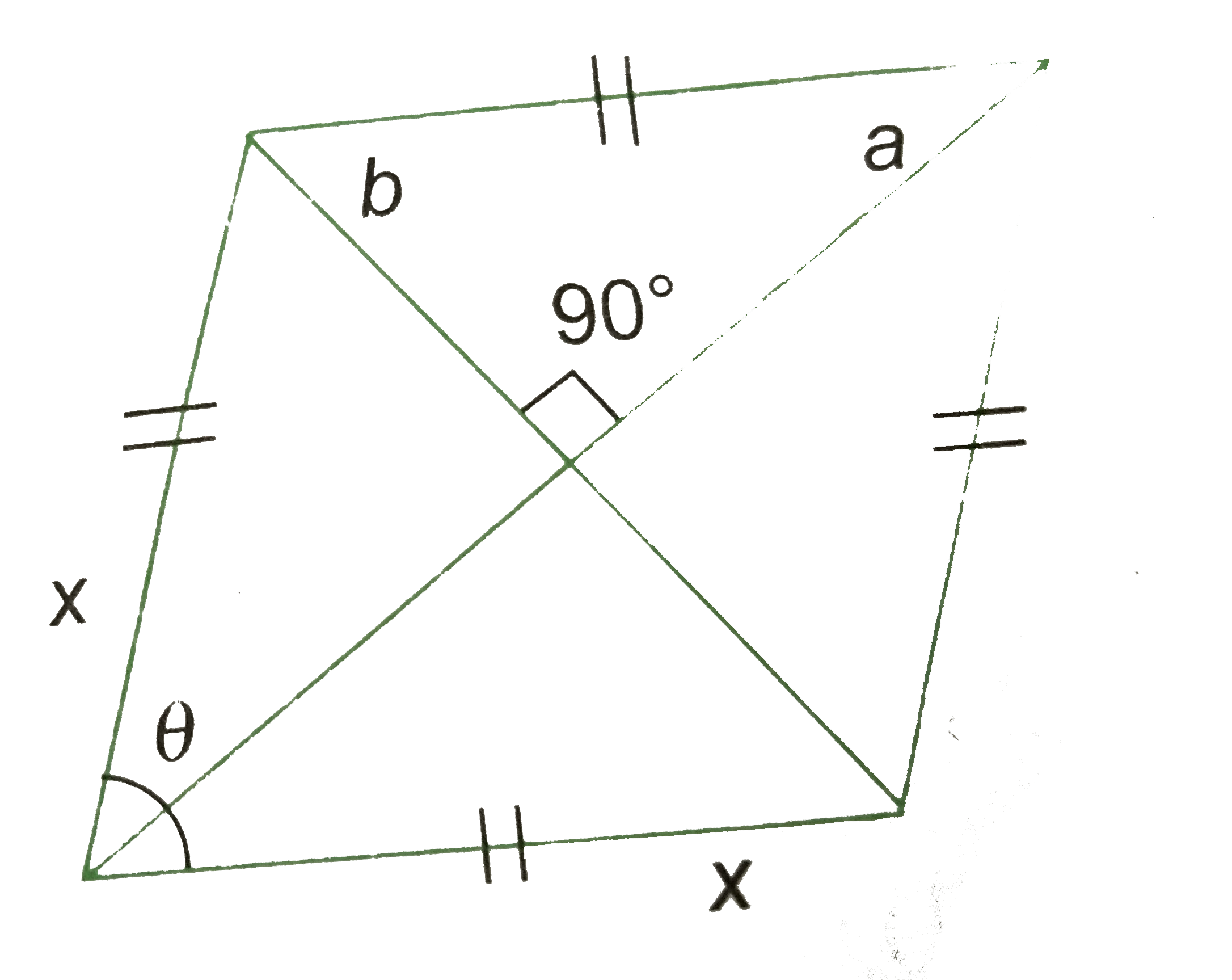
Given that the side length of a rhombus is the geometric mean of the length of its diagonals. The degree measure of the acute angle of the rhombus is 150 (b) 300 (c) 450 (d) 600Solution in Bengali
15∘
30∘
45∘
60∘
The correct Answer is:B
Area of rhomubs is given by
2×12x2sinθ=ab2 (Equating area of a rhombus)
Given x2=ab (given)
⇒sintη=12
orθ=30∘
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Correct Answers Type17videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Linked Comprehension Type11videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Concept Application Exercises 2.141videos
TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)4videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)2videos
TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULAS
Similar Questions
If 0≤θ≤πand81sin2θ+81cos2θ=30 is
02:38View SolutionLet us consider the equation cos^4x/a xa+sin4xb=1a+b,x∈[0,π2],a,b>0 the value of sin8xb3+cos8xa3 is
02:56View SolutionIf any quadrilateral ABCD, prove that sin(A+B)+sin(C+D)=0 cos(A+B)=cos(C+D)
07:05View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
07:56View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
04:43View SolutionGiven that the side length of a rhombus is the geometric mean of the length of its diagonals. The degree measure of the acute angle of the rhombus is (a)150 (b) 300 (c) 450 (d) 600
03:20View SolutionThe angle between sides of a rhombus whose v2xx sides is mean of its two diagonal,is equal to: a)30^(@)(b)45^(@)(c)60^(@)(d)90^(@)
01:32View SolutionThe acute angle of a rhombus whose side is a mean proportional between its diagonals is
13:07View SolutionThe area of the rhombus ABCD is 24. The equation of the diagonal BD is 4x + 3y + 2=0 and A (3,2) The length of the side of the rhombus is
02:45View SolutionGiven that the side length of a rhombus is the geometric mean of the length of its diagonals. The degree measure of the acute angle of the rhombus is (a)150 (b) 300 (c) 450 (d) 600
01:33View SolutionIf the hypotenuse of a right-angled triangle is four times the length of the perpendicular drawn from the opposite vertex to it, then the difference of the two acute angles will be 600 (b) 150 (c) 750 (d) 300
03:11View SolutionGiven that the side length of a rhombus is the geometric mean of the length of its diagonals. The degree measure of the acute angle of the rhombus is 150 (b) 300 (c) 450 (d) 600
04:57View SolutionThe acute angle of a rhombus whose side is a mean proportional between its diagonals is
08:03View SolutionA rhombus of side 20cm has two angles of 600 each. Find the length of the diagonals.
View SolutionIf two acute angles of a right triangle are equal, then each acute is equal to (a)300 (b) 450 (c) 600 (d) 900
01:30View SolutionGiven that the side length of a rhombus is the geometric mean of the lengths of its diagonals. The degree measure of the acute angle of the rhombus is
02:54View Solution

