If f:[−3,4]→R,f(x)=2x, and g:[−2,6]→R,g(x)=x2. Then find function (f+g)(x).Solution in Bengali
f:[−3,4]→R,f(x)=2x, and g:[−2,6]→R,g(x)=x2
For (f+g)(x) we consider common domain of f(x) and g(x).
Now [−3,4]∩[−2,6]≡[−2,4]
So, (f+g):[−2,4]→R,(f+g)(x)=2x+x2.
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
02:20View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 601:10View SolutionFind gof and gof when f:R→R and g:R→R is defined by f(x)=2x+x2 and g(x)=x3
01:49View SolutionIf f,g:R→R be defined by f(x)=2x+1 and g(x)=x2−2,∀x∈R, respectively. Then , find gof .
03:39View SolutionIf f:[−3,4]→R,f(x)=2x, and g:[−2,6]→R,g(x)=x2. Then find function (f+g)(x).
02:22View SolutionLet f:R→R:f(x)=x2+2and g:R→R:g(x)=xx−1,x≠1. Find f o g and g o f and hence find (f o g) (2) and ( g o f) (-3)
03:19View Solutionमान लीजिए कि f,g:R→R क्रमश: f(x)=x+1,g(x)=2x−3 द्वारा परिभाषित है।
(f+g)(x),(f−g)(x) और (fg)(x) ज्ञात कीजिए।02:32View Solutionयदि फलन f:R→R,f(x)=2x+1 एवं g:R→R,g(x)=x2−2 द्वारा परिभाषित हों, तो दशाईए कि gof ≠ fog.
02:49View SolutionIf f,g:R→R be defined by f(x)=2x+1 and g(x)=x2−2,∀x∈R, respectively. Then , find gof .
03:55View SolutionIf f:[−3,4]→R,f(x)=2x, and g:[−2,6]→R,g(x)=x2. Then find function (f+g)(x).
00:52View SolutionFind gof and fog when f:R→R and g:R→R is defined by f(x)=2x+x2 and g(x)=x3
01:34View SolutionIf f:R→R,f(x)=x−2,g:R→R,g(x)=x+2 then (f+g)(x)= ……..
01:31View SolutionA table of values of f, g, f' and g' is given:
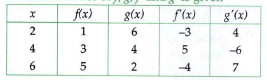 . If r(x) = f[g(x)], find r'(2)04:08View Solution
. If r(x) = f[g(x)], find r'(2)04:08View SolutionIf f,g : R→R such that f(x)=3x2−2,g(x)=sin(2x) the gof=
05:00View SolutionA table of values of f,g, f' and g' is given:-
 If r(x)= f(g(x)), find r'(2).02:00View Solution
If r(x)= f(g(x)), find r'(2).02:00View SolutionIf f:R→R and g:R→R are defined by f(x)=2x2+3 and g(x)=3x−2, then find:
(i) (fog)(x), (ii) (gof)(x), (iii) (fof)(0), (iv) (go(fof))(3)02:19View Solution

