ABCD is a square of side l. A line parallel to the diagonal BD at a distance 'x' from the vertex A cuts two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x. Find this area at x=1/√2 and at x=2, when l=2.Solution in Bengali
There are two cases
Case -I : when x=AP≤OA,i.e.,x≤l√2
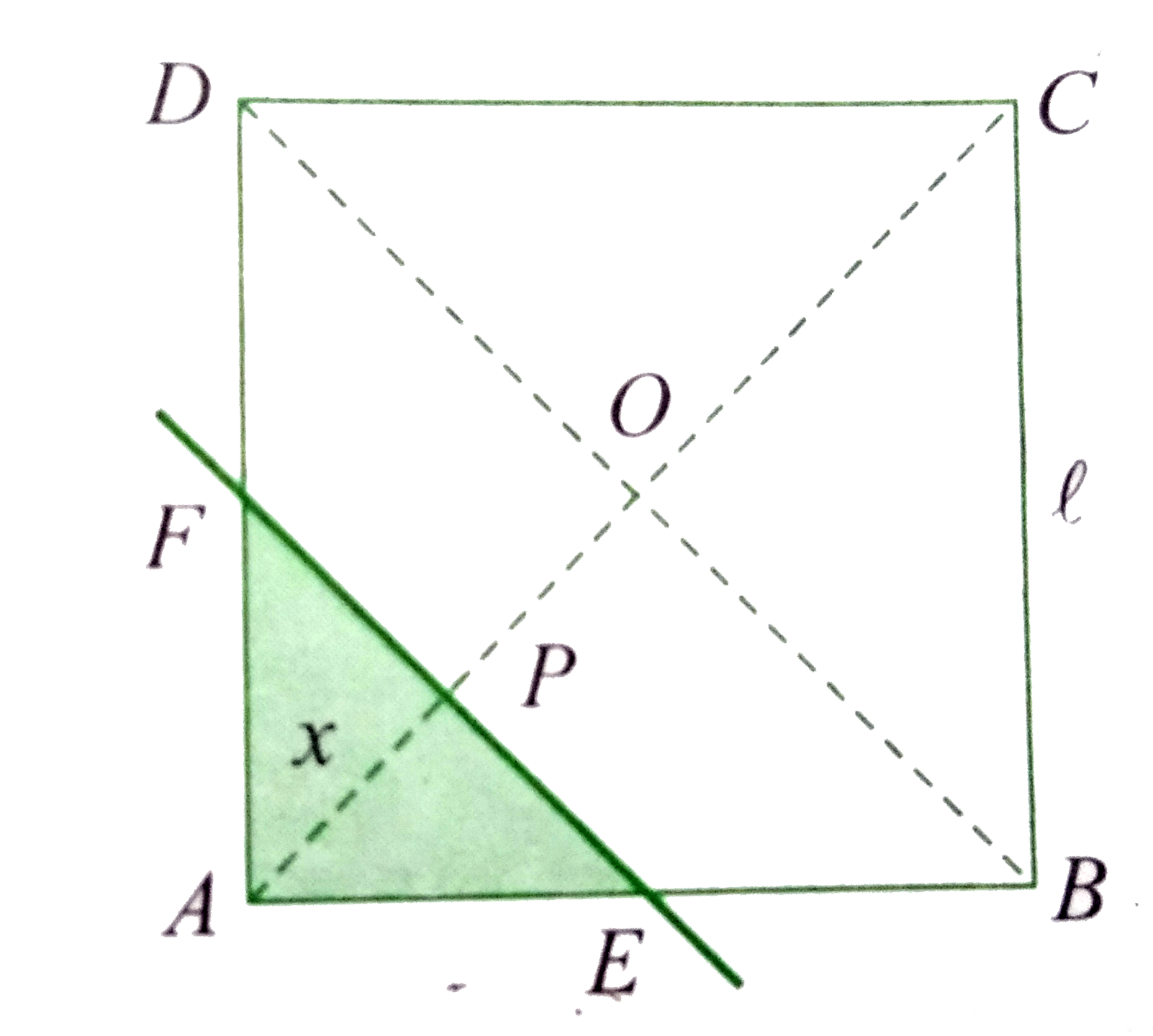
∴Ar(△AEF)=12x,2x=x2 (∵PE=PF=AP=x)
Case-II : when x=AP>OA,i.e.,x>l√2 but x≤√2l

ar(ABEFDA)=ar(ABCD)−ar(△CFE)
=l2−12(√2l−x)⋅2(√2l−x) [∵CP=√2l−x]
=l2−(2l2+x2−2√2lx)=2√2lx−x2−l2
So, the required function s(x) is
s(x)=⎧⎪⎨⎪⎩x2, 0≤x≤l√22√2lx−x2−l2,l√2<x≤√2l
∴s(x)=⎧⎪⎨⎪⎩12 at x=1√28(√2−l) at x=2
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 603:45View SolutionABCD is a square of side l. A line parallel to the diagonal BD at a distance 'x' from the vertex A cuts two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x. Find this area at x=1/√2 and at x=2, when l=2.
View SolutionABCD is a square of side a. A line parallel to the diagonal BD at a distance x from the vertex A cuts the two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x.
05:14View SolutionABCD is a square of side length 2 units. C1 is the circle touching all the sides of the square ABCD and C2 is the circumcircle of square ABCD. L is a fixed line in the same plane and R is fixed point.
A line L' through a is drawn parallel to BD. Point S moves scuh that its distances from the line BD and the vertex A are equal. If loucs S cuts L' at T2andT3 and AC at T1, then area of ΔT1T2T3 is02:43View SolutionLet ABCD be a square of side length 2 units. C_(2) is the circle through vertices A, B, C, D and C_(1) is the circle touching all the sides of the square ABCD. L is a line through A A line M through A is drawn parallel to BD. Point S moves such that its distances from the line BD and the vertex A are equal. If locus of S cuts. M at T_(2) and T_(3) and AC at T_(1) , then area of DeltaT_(1)T_(2)T_(3) is
07:13View Solutionवर्ग ABCD का एक शीर्ष A मूलबिंदु है । यदि वर्ग की भुजाएँ AB और AD क्रमश : x-अक्ष और y-अक्ष हों और वर्ग की भुजा a हो , तो वर्ग के शीर्षों के निर्देशांक बताइए ।
View SolutionThe diagonal of a square is 8x- 15y =0 and one vertex of the square is (1, 2). The equations to the sides of the square passing through this vertex are
07:13View SolutionThe diagonal of a square is 8x- 15y =0 and one vertex of the square is (1, 2). The equations to the sides of the square passing through this vertex are
14:49View SolutionThe diagonal of a square is 8x- 15y =0 and one vertex of the square is (1, 2). The equations to the sides of the square passing through this vertex are
03:41View SolutionABCD is a square of side l. A line parallel to the diagonal BD at a distance 'x' from the vertex A cuts two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x. Find this area at x=1/√2 and at x=2, when l=2.
02:27View SolutionIf x and y are the sides of two squares such that y=x−x2. Find the change of the area of second square with respect to the area of the first square.
03:36View SolutionIf x and y are the sides of two squares such that y=x−x2. Then the rate of change, if the area of second square with respect to the first square, when x = 2, is ……….
14:56View SolutionTake a square ABCD of side l and BD is diagnol. Find MOI along a line passing through corner parallel to BD
04:01View Solutionएक वर्ग ABCD के सभी शीर्ष वक्र x2y2=1 पर हैं। इसकी भुजाऐं के मध्यबिंदु भी इसी वक्र पर हैं तो ABCD के क्षेत्रफल का वर्ग है "____________"।
02:29View Solution

