Solve sinx>−12Solution in Bengali
The correct Answer is:(a) ∪n∈Z(nπ−π2,nπ+tan−12)
(b) ∪n∈Z[2nπ+2π3,2nπ+4π3]
(a) We know that tanx is periodic with period π. So, check the solution in the interval (−π2,π2).
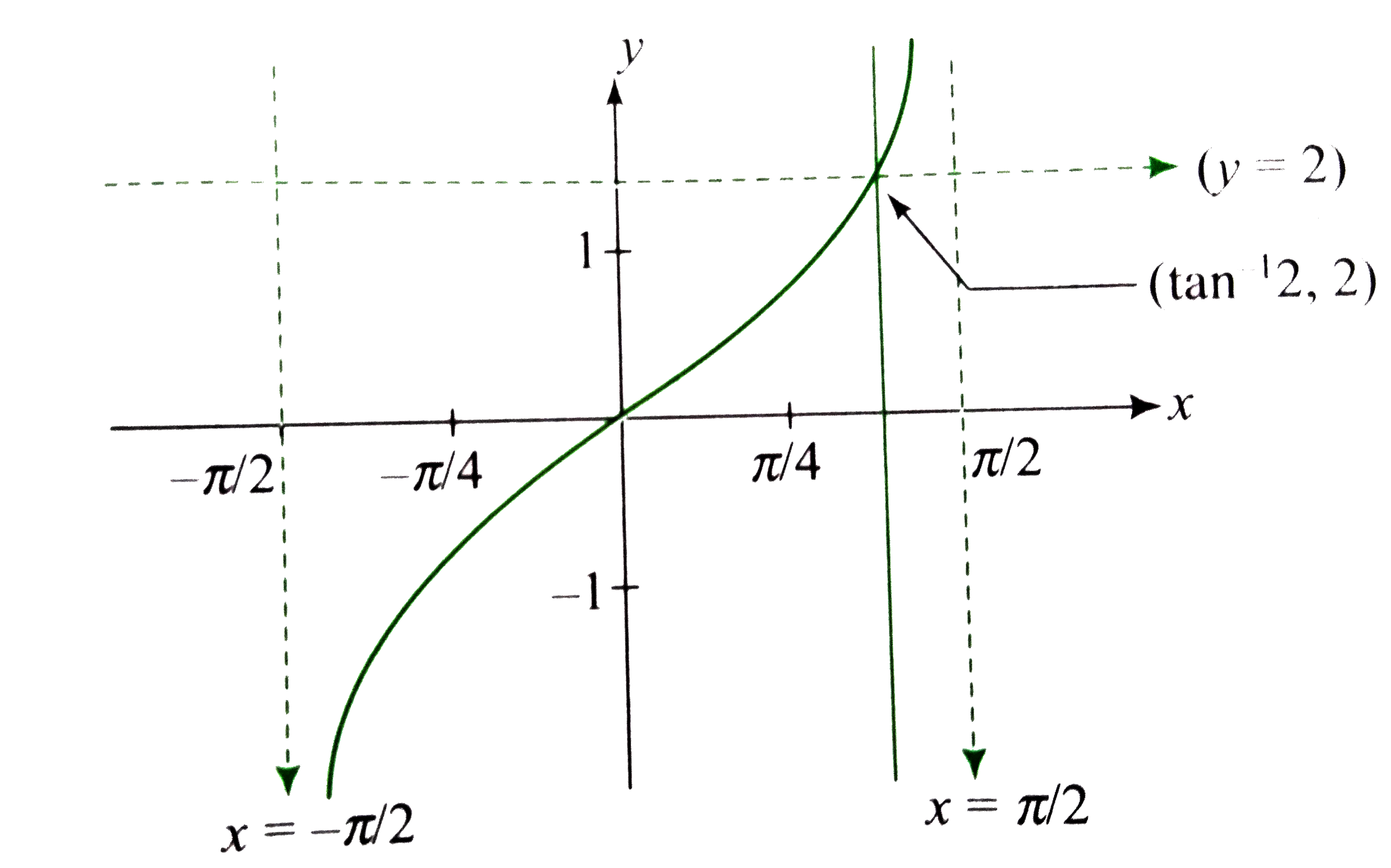
It is clear from the figure that tanx<2 when
−π2<x<tan−12.
Therefore, general solution is
∪n∈Z(nπ−π2,nπ+tan−12)
(b) cosx is periodic with period 2π.
So, check the solution in [0,2π].

It is clear from the figure that cosx≤−12 when
2π3≤x≤4π3.
On generalizing the above solution, we get
x∈∪n∈Z[2nπ+2π3,2nπ+4π3]
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
02:37View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 603:26View Solutionहल करें
sinx+cosx=√2View Solutionहल करें
2cosx+sinx=102:24View Solutionsolve ∣∣x2−1+sinx∣∣=∣∣x2−1∣∣+|sinx|, where x∈[−2π,2π].
02:11View Solutionसमीकरण |sinx|=12 को हल कीजिए ।
01:33View SolutionSolve sinx +cosx =1
02:42View SolutionSolve sinx>−12
03:27View SolutionSolve the equation sinx+cosx=1
02:23View SolutionSolve: ∣∣−2x2+1+ex+sinx∣∣=∣∣2x2−1∣∣+ex+|sinx|,x∈[0,2π].
02:01View SolutionSolve:
tan−1(cosx−sinxcosx+sinx)03:52View SolutionSolve ∣∣ ∣ ∣∣ysinxcosxcosx1y−sinx−y1∣∣ ∣ ∣∣
04:41View SolutionSolve :√3cosx−sinx=1
04:35View SolutionSolve: 2tan−1(sinx)=tan−1(2secx),x≠π2.
04:45View SolutionSolve sinx>−12
05:35View SolutionSolve: ∣∣−2x2+1+ex+sinx∣∣=∣∣2x2−1∣∣+ex+|sinx|,x∈[0,2π].
01:24View Solution

