Prove that the least positive value of x, satisfying tanx=x+1,liesintheinterval(π4,π2).Solution in Bengali
Let f(x)=tanx and g(x)=x+1, which can be shown as follows.
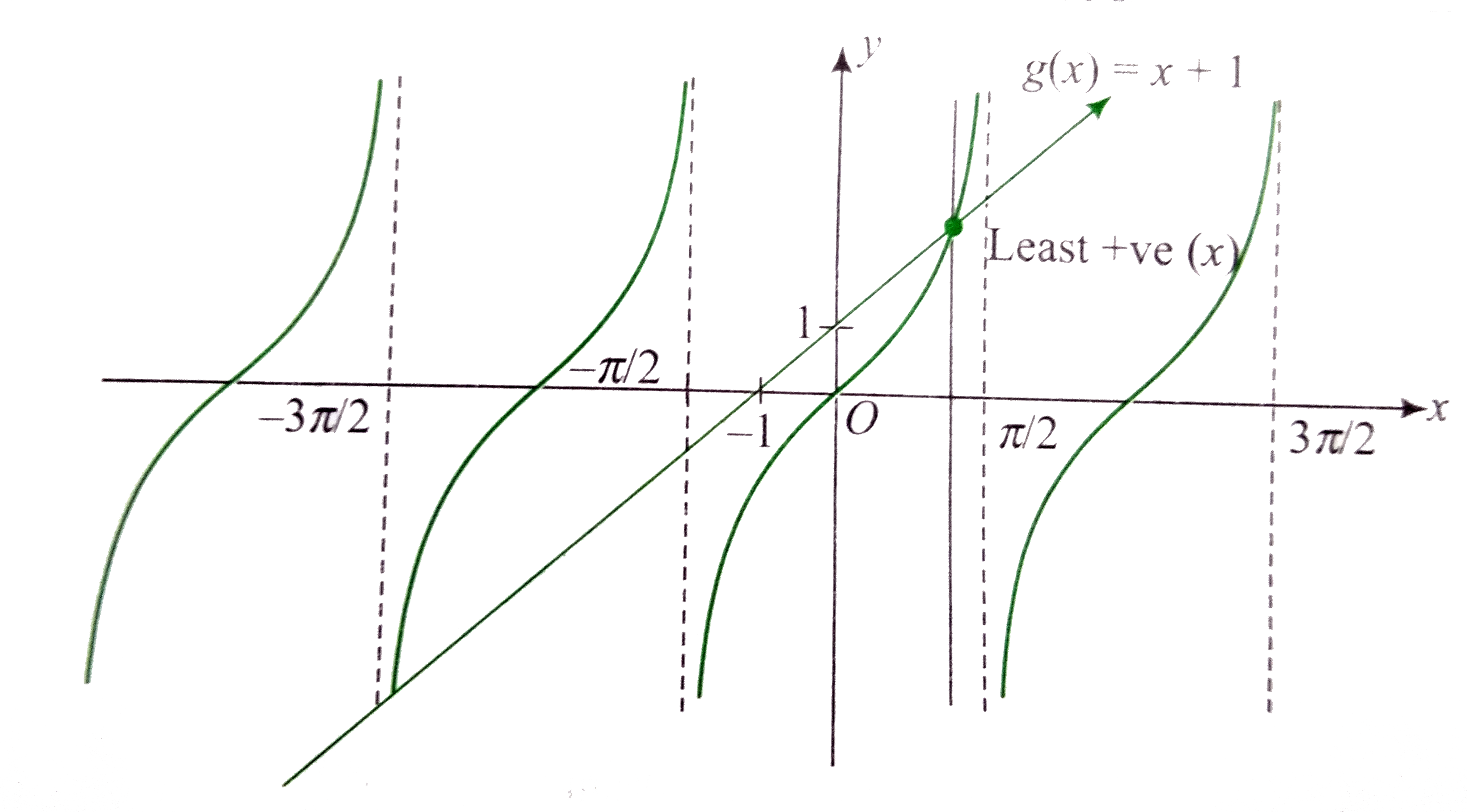
From the figure, tanx=x+1 has infinitely many solutions but the least positive value of x lies in (π4,π2).
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
04:24View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 603:10View SolutionProve that the least positive value of x, satisfying tanx=x+1, lies in the interval (π4,π2)
03:10View SolutionProve that the least positive value of x, satisfying tanx=x+1,liesinthe∈terval(π4,π2).
01:57View Solutionसाबित करें कि tan(π4+x)tan(π4−x)=(1+tanx1−tanx)2
02:07View Solutionसिद्ध कीजिए कि : tan(π4+x)=1+tanx1−tanx
03:02View Solutionसिद्ध कीजिए कि : tan(π4−x)=1−tanx1+tanx
04:13View SolutionProve that tan(π4+x)tan(π4−x)=(1+tanx1−tanx)2
03:30View SolutionProve that:tan(π4+x)tan(π4−x)=(1+tanx1−tanx)2
03:23View SolutionProve that the least positive value of x, satisfying tanx=x+1, lies in the interval (π4,π2)
02:58View SolutionProve that the least positive value of x, satisfying tanx=x+1,liesintheinterval(π4,π2).
04:06View SolutionProve that the least positive value of x, satisfying tanx=x+1, lies in the interval (π4,π2)
04:15View SolutionProve that the least positive value of x, satisfying tanx=x+1,liesinthe∈terval(π4,π2).
02:05View SolutionUsing mean value theorem, prove that tanx>x for all x(0,π2).
05:32View SolutionProve that
tan(π4+x)tan(π4−x)=(1+tanx1−tanx)204:11View Solutionprove that
tan(π4+x)tan(π4−x)=(1+tanx1−tanx)202:29View Solution

