Find the area bounded by y=tan−1x,y=cot−1x,andy−aξs in the first quadrant.Solution in Bengali
The correct Answer is:log√2 sq. units
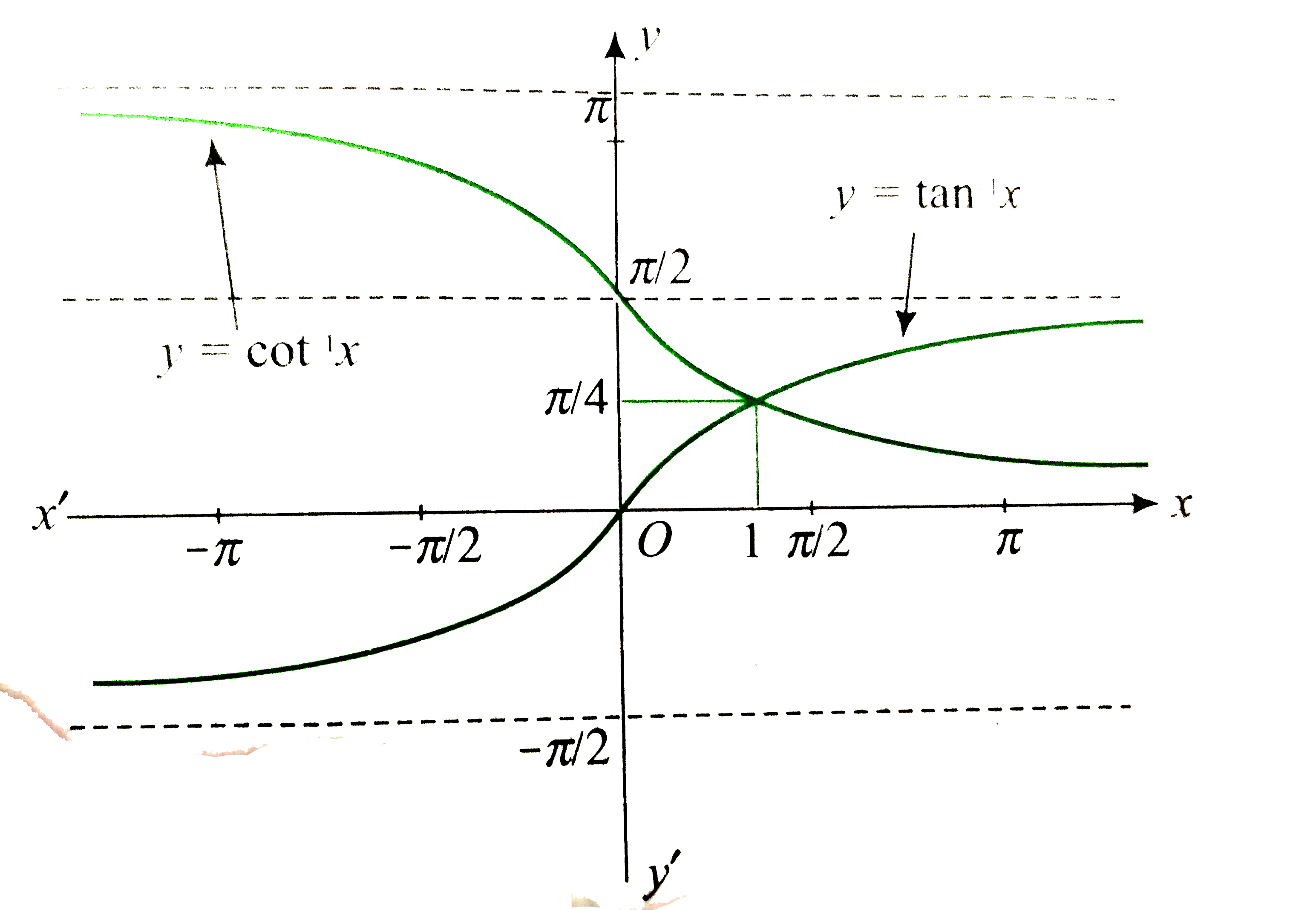
Intergrating along x-axis, we get
A=1∫0(cot−1x−tan−1x)dx=1∫0(π2−2tan−1x)dx
Intergrating a long y-axis, we get
A=2π/4∫0xdy=2.π/4∫0tanydy=[log(secy)]π/40
=log√2 sq. units
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.37videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Exercises - Single Correct Answer Type40videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.19videos
AREA
- BOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type2videos
APPLICATIONS OF DERIVATIVES
- BOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension11videos
BINOMIAL THEOREM
Similar Questions
Find the continuous function f where (x4−4x2)≤f(x)≤(2x2−x3) such that the area bounded by y=f(x),y=x4−4x2. then y-axis, and the line x=t, where (0≤t≤2) is k times the area bounded by y=f(x),y=2x2−x3,y-axis , and line x=t(where0≤t≤2).
02:11View SolutionArea enclosed by the curve y=f(x) defined parametrically as x=1−t21+t2,y=2t1+t2isequa<o πsq.units (b) π2sq.units 3π4sq.units (d) 3π2sq.units
06:57View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
02:27View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
02:03View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is03:38View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2,x=0,y=1andy=4.
03:32View SolutionFind the area bounded by y=tan−1x,y=cot−1x,and y-axis in the first quadrant.
02:16View SolutionFind the area of the region bounded by x2=16y, y=1, y=4 and the y-axis in the first quadrant.
04:46View SolutionFind the area bounded by the curve y=4x^(2),x=0,x=1 and y=4 in first quadrant.
03:35View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2, x = 0, y = 1 and y = 4.
02:55View SolutionFind the area of the region lying in the first quadrant and bounded by y=4x2, x = 0, y = 1 and y = 4.
View SolutionFind the area of the region lying in the first quadrant and bounded by y = 4x^(2), x = 0, y = 1 and y = 4.
06:04View SolutionFind the area bounded by y=tan−1x,y=cot−1x,and y-axis in the first quadrant.
02:31View SolutionFind the area of the region bounded by x2=16y, y=1, y=4 and the y-axis in the first quadrant.
04:36View SolutionFind the area of the region lying in the first quadrant and bounded by y = 4x^(2), x = 0, y = 1 and y = 4.
04:20View SolutionFind the area of the region lying in the first quadrant and bounded by y = 4x^(2), x = 0, y = 1 and y = 4.
03:33View Solution
