If $A_{i}$ is the area area bounded by $| x - a_{i} | + | y | = b_{i}, i \in N$ ,where $a_{i + 1} = a_{i} + \frac{3}{2} b_{i} and b_{i + 1} = \frac{b_{i}}{2}, a_{1} = 0 and b_{1} = 32$ , thenSolution in Bengali

A

A. $A_{3} = 128$

B

B. $A_{3} = 256$

C

C. $lim n \to \infty n Σ i = 1 A_{i} = \frac{8}{3} {(32)}^{2}$

D

D. $lim n \to \infty n Σ i = 1 A_{i} = \frac{4}{3} {(16)}^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, C

$a_{1} = 0, b_{1} = 32, a_{2} = a_{1} + \frac{3}{2} b_{1} = 48, b_{2} = \frac{b_{1}}{2} = 16$
$a_{3} = 48 + \frac{3}{2} \times 16 = 72, b_{3} = \frac{16}{2} = 8$

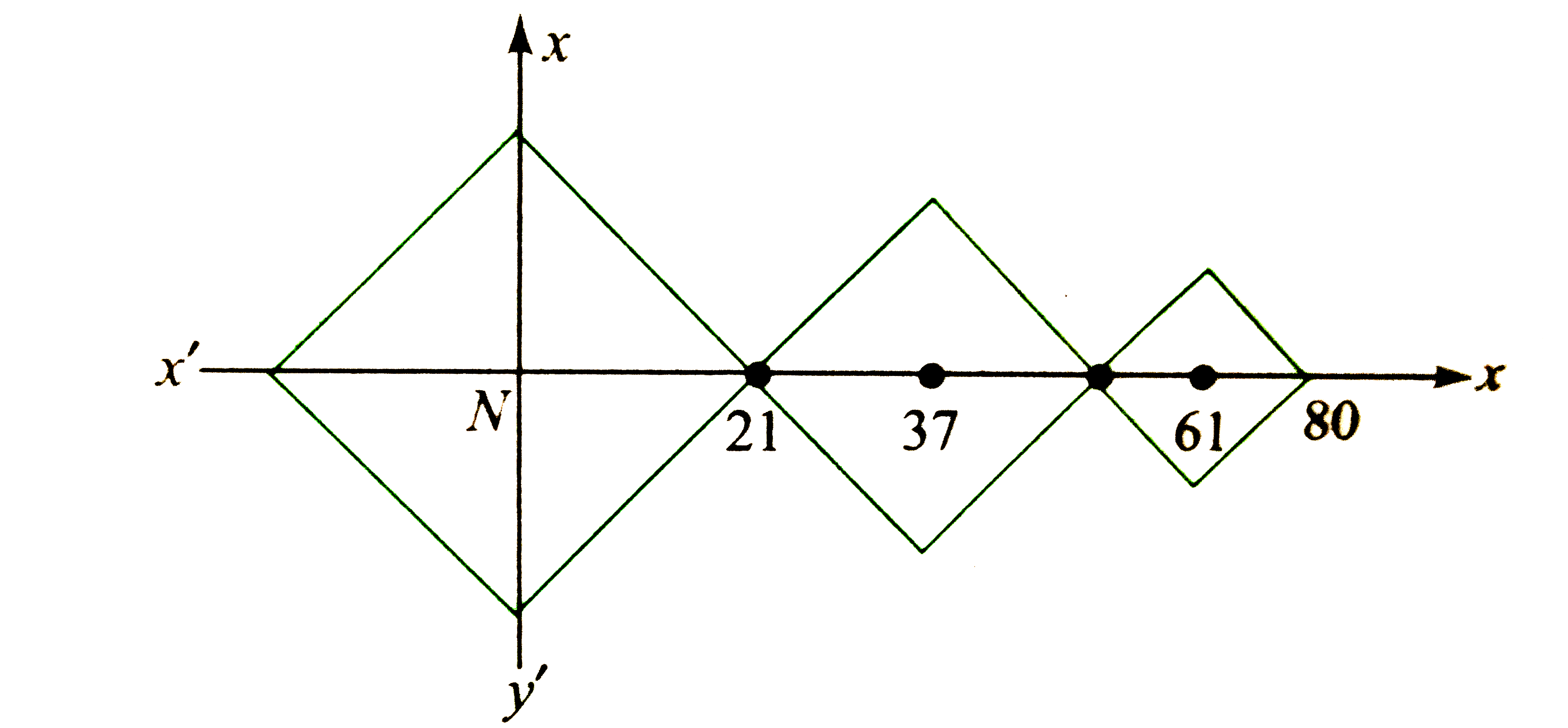
So the three loops from i=1 to i=3 are alike.
Now area of ith loop (square) $= \frac{1}{2} {(diagonal)}^{2}$
$A_{i} = \frac{1}{2} {(2 b_{i})}_{i}^{2} = 2 {(b_{i})}_{i}^{2}$
$S o, \frac{A_{i} + 1}{A_{i}} = \frac{2 {(b_{i + 1})}_{i + 1}^{2}}{2 {(b_{i})}_{i}^{2}} = \frac{1}{4} .$
So the areas from a G.P. series.
So, the sum of the G.P. up to infinite terms is
$A_{1} \frac{1}{1 - r} = 2 {(32)}^{2} \times \frac{1}{1 - \frac{1}{4}}$
$= 2 \times {(32)}^{2} \times \frac{4}{3} = \frac{78}{3} {(32)}^{2}$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

CENGAGE PUBLICATION-AREA-Multiple Correct Answers Type

Home
Ask Doubt
Profile