Question

-q, and d-s, then the correctly bubbled $4x4$
matrix should be as follows:
Figure:
of
the region lying between the lines $x-y+2=0,x=0$
and the curve
$x=\sqrt{y}$
, q. 64/3 sq.
units
The area
enclosed between the curves $y^2=xandy=\left|x\right|$
, r. 2/3 sq.
units
The area
bounded by parabola $y^2=x,$
straight line
$y=4,andthey-a\xi s$
, s. 1/6 sq.
units

Answer

8

Explanation

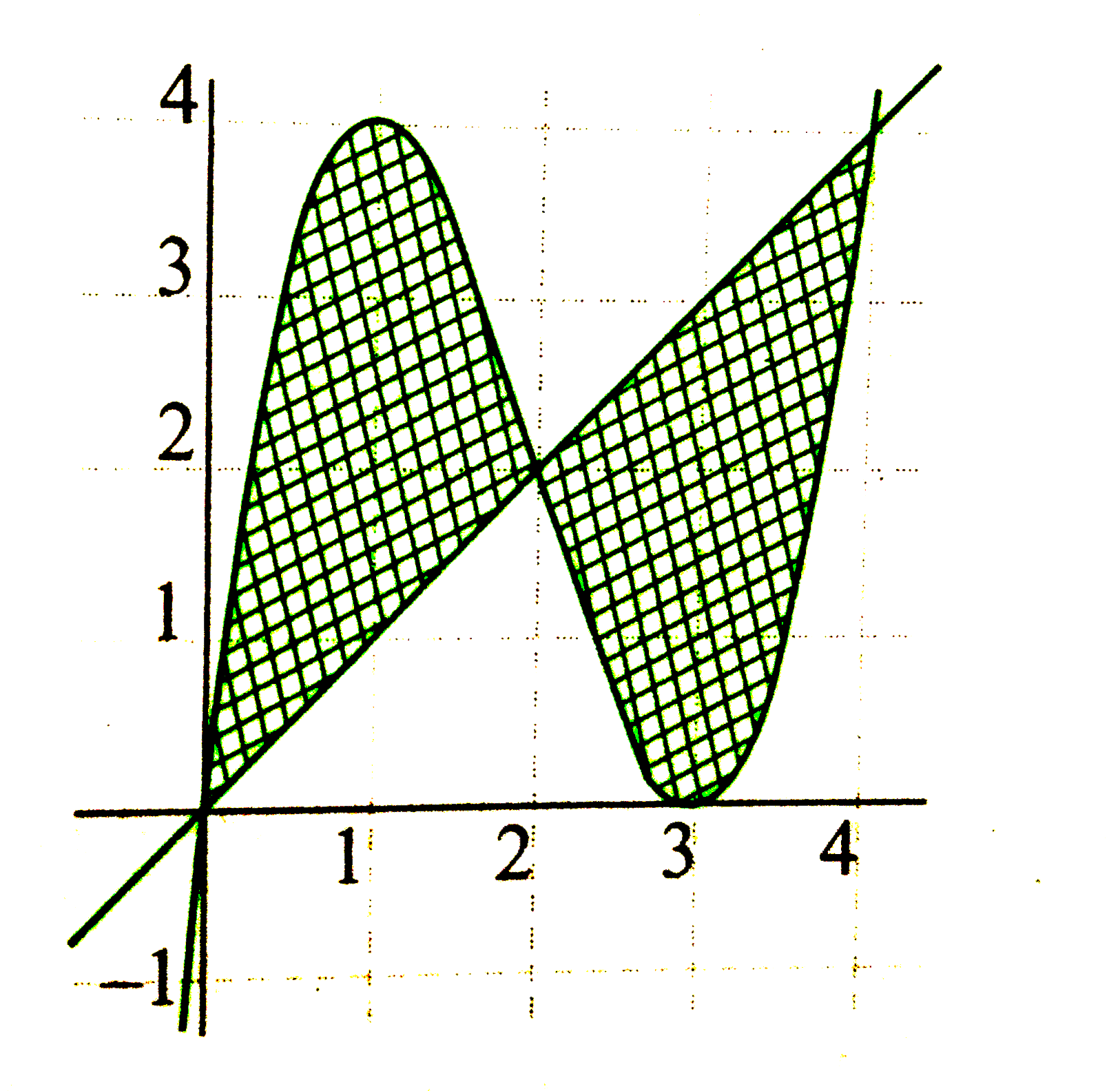
`"Required area "=2int_(0)^(2)(x(x-3)^(2)-x)_dx=8` sq. units