For a point in the plane, let be the distances of the point from the lines respectively. The area of the region consisting of all points lying in the first quadrant of the plane and satisfying isSolution in Bengali
The correct Answer is:6
For P(x,y), we have
IN first quadrant if we have
The region of points satisfying these inequalities is
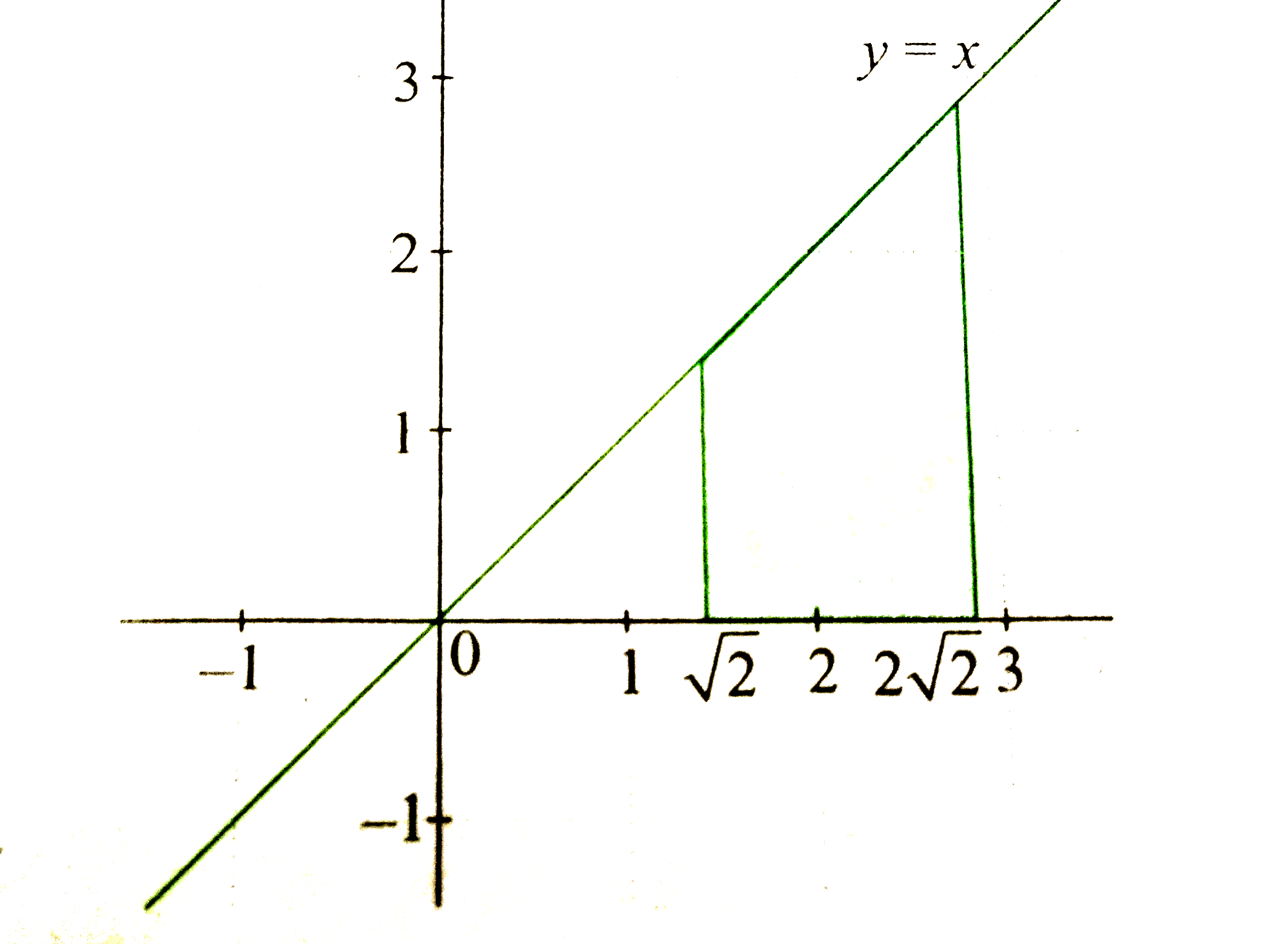
In first quadrant if , we have
The region of points satisfying these inequalities is
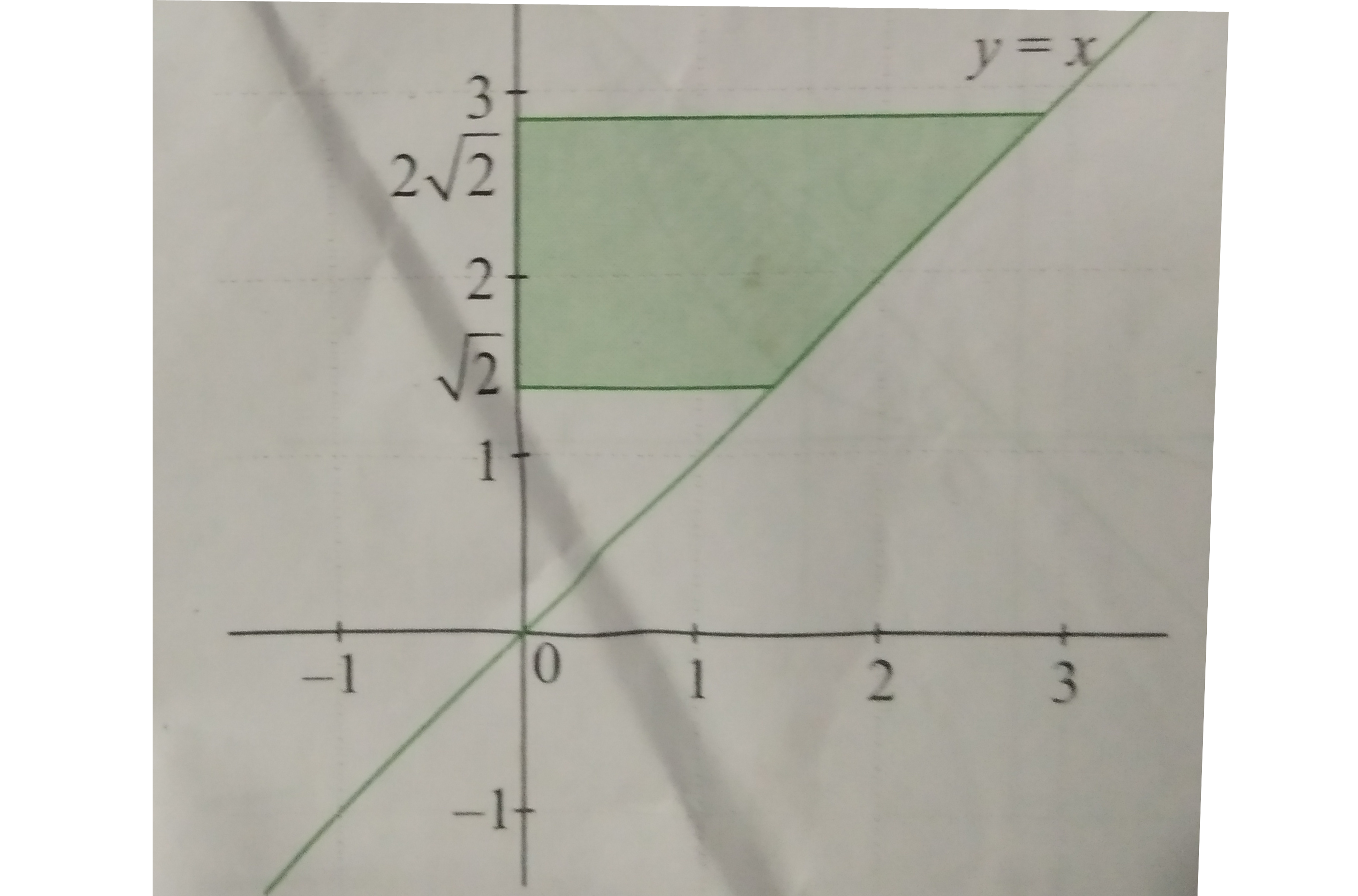
Combining above two regions we have

Area of the shaded region
sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Archives
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Single Correct Answer Type
30 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Matrix Match Type
5 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
The area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate x=3, and the x−aξs is 7sq.unites (b) 6sq.unites 9sq.unites (d) None of these
View SolutionLet the straight line x= b divide the area enclosed by y=(1−x)2,y=0,andx=0 into two parts R1(0≤x≤b)andR2(b≤x≤1) such that R1−R2=14. Then b equals
View SolutionMatch the following lists :

View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionFor a point P in the plane, let d1 (P) and d2 (P) be the distance of the point P from the lines x – y = 0 and x + y = 0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2 < d1(P) + d2 (P)< 4, is
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionConsider two lines L1andL2 given by x−y=0 and x+y=0 , respectively, and a moving point P(x,y). Let d(P,L1),i=1,2, represents the distance of point P from the line Lt If point P moves in a certain region R in such a way that 2≤d(P,P1)+d(P,L1)≤4 , find the area of region R.
View SolutionFor a point P(x,y),x<=2 in x-y plane moves on path y=|ax-1|+|ax-2|+ax AA alpha in[0,1] If area of region R consisting of all points P lying in the first quadrant of the plane is A when take it's all values alpha in[0,1], then value of (6)/(A) is
View SolutionFor a point P in the plane let d1(P)andd2 be the distance of the point P from the lines x−y=0 R consisting of all points P lying in the first quadrant of the plane and satisfying 2≥d1(P)+d2(P)≥4, is
View SolutionFor a point P in the plane, let d1(P) and d2(P) be the distances of the point P from the lines x−y=0 and x+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View Solutionसमतल में स्थित किसी बिन्दु P से रेखाओ x - y = 0 तथा x + y = 0 की दुरी क्रमशः d1(P) तथा d2(P) है। यदि क्षेत्र R उन सभी बिन्दुओ P से बना है जो प्रथम चतुर्थांश (quadrant) में स्थित है तथा 2≤d1(P)+d2(P)≤4 को संतुष्ट करते है, तब क्षेत्र R का क्षेत्रफल है
View SolutionFor a point P in the XY plane.Let d1(p),d2(p) and d3(p) be the distances of the point P from the x axis,y axis and x−y=0 respectively. If A is area of the region R consisting of all points P lying in the XY plane and satisfying d1(P)+d2(P)+√2d3(P)=5 then Which of the following is/are CORRECT
View Solutionসমতল p:x−y+z=5 এবং একটি বিন্দু P(1,−2,3)P বিন্দু থেকে সমতল p-এর দূরত্ব-
View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
View SolutionConsider two lines L1andL2 given by x−y=0 and x+y=0 , respectively, and a moving point P(x,y). Let d(P,L1),i=1,2, represents the distance of point P from the line Lt If point P moves in a certain region R in such a way that 2≤d(P,L1)+d(P,L2)≤4 , find the area of region R.
View Solution
