The locus of the foot of the perpendicular from the origin on each member of the family (4a+3)x−(a+1)y−(2a+1)=0 (a) (2x−1)2+4(y+1)2=5 (b) (2x−1)2+(y+1)2=5 (c) (2x+1)2+4(y−1)2=5 (d) (2x−1)2+4(y−1)2=5 Solution in Bengali
(2x−1)2+4(y+1)2=5
(2x−1)2+(y+1)2=5
(2x+1)2+4(y−1)2=5
(2x−1)2+4(y−1)2=5
The correct Answer is:C
Given family of lines is (4a+3)x−(a+1)y−(2a+1)=0
or (3x−y−1)+a(4x−y−2)=0
Family of lines passes through the fixed point P which is the intersection of
3x−y=1 and 4x−y=2
Solving we get P(1,2).
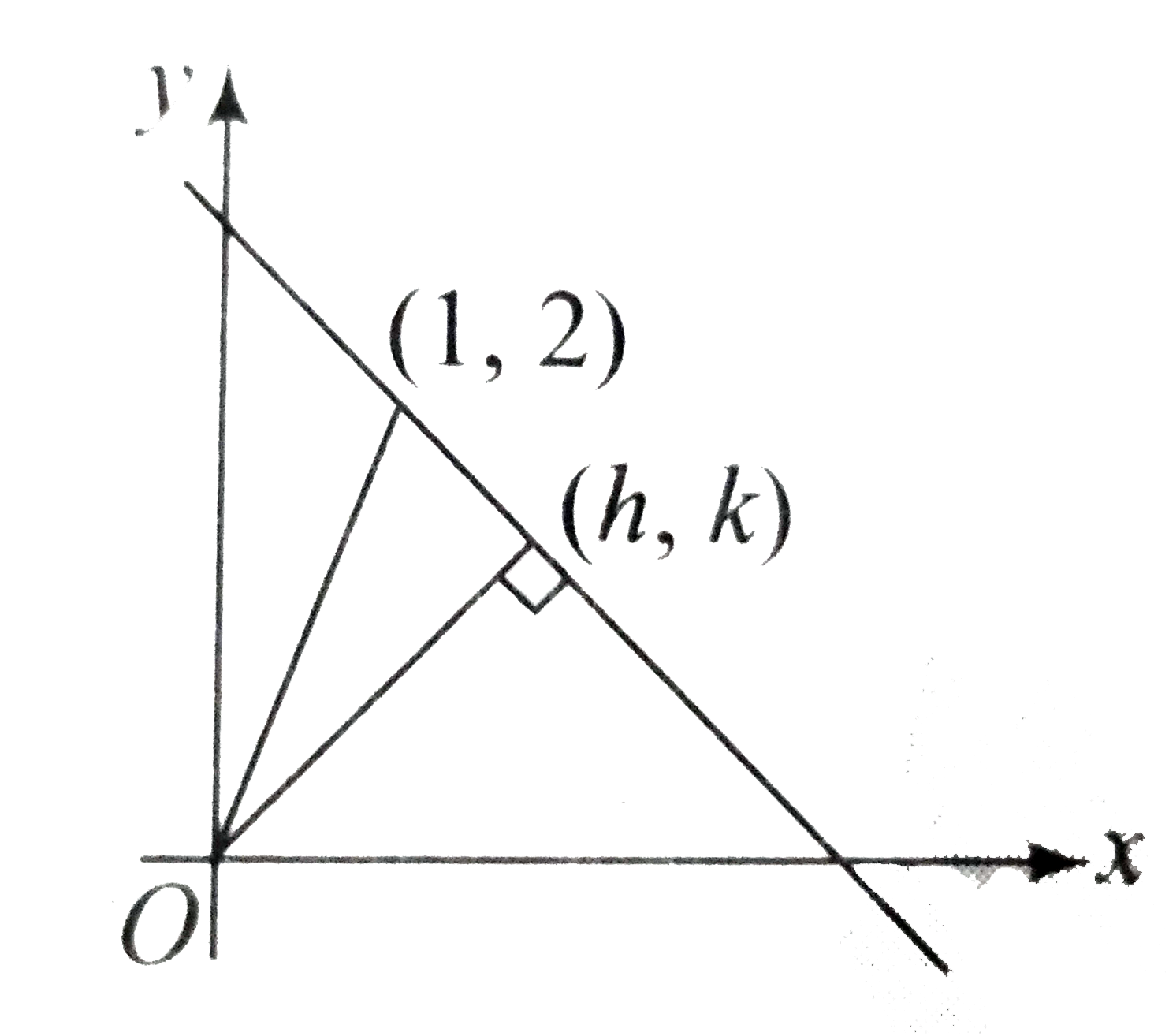
Now let (h,k) be the foot of perpendicular on each of the family.
∴kh.k−2h−1=−1
∴ Locus is x(x−1)+y(y−2)=0
or (2x−1)2+4(y−1)2=5
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE PUBLICATIONCHAPTER - STATISTICSEXERCISE - Archives10videos
STATISTICS
- BOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)1videos
STRAIGHT LINES
Similar Questions
The point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
06:51View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
03:20View SolutionIf the mean deviation of the numbers 1,1+d,1+2d,...,1+100d from their mean is 255, then the d is equal to
04:41View SolutionFor a point P in the plane, let d1(P)andd2(P) be the distances of the point P from the lines x−y=0andx+y=0 respectively. The area of the region R consisting of all points P lying in the first quadrant of the plane and satisfying 2≤d1(P)+d2(P)≤4, is
04:30View SolutionIf x3−2x2y2+5x+y−5=0 and y(1)=1, then (a)y′(1)=43 (b) y'(1)=−43 (c)y''(1)=−82227 (d) y′(1)=23
05:30View Solutionif xy^(4)=2x^(2)y^(3)-y^((1)/(3))-5 at (dy)/(dx) at (1,-1)
07:24View SolutionFind the products: (i) (2x+y)(2x−y)(4x2+y2)
07:09View Solutionx^(3)-2x^(2)y^(2)+5x+y-5=0, then find (d^(2)y)/(dx^(2)) at x=1,y=1
08:12View Solution[" The solution of "(dy)/(dx)=(1)/(2x-y^(2))" is given by "],[[" (A) "y=Ce^(-2x)+(1)/(4)x^(2)+(1)/(2)x+(1)/(4)," (B) "x=Ce^(-y)+(1)/(4)y^(2)+(1)/(4)y+(1)/(2)],[" (C) "x=Ce^(y)+(1)/(4)y^(2)+y+(1)/(2)," (D) "x=Ce^(2y)+(1)/(2)y^(2)+(1)/(2)y+(1)/(4)]]
04:35View SolutionThe solution ofdydx=12x−y2 is given by , (A)y=Ce−2x+14x2+12x+14, 412, (B) x=Ce−y+14y2+14y+12, (C) x=Cey+14y2+y+12, (D) x=Ce2y+12y2+12y+14
05:13View Solutionयदि y=2x2−1 तो सिद्ध कीजिए की
1x2+12x4+13x6+...........=2(1y+13y3+15y5+.........)04:44View SolutionIf x2−2x2y2+5x+y−5=0andy(1) then y''(1)=
02:37View SolutionThe equation of the transvers and conjugate axes of a hyperbola are, respectively, x+2y−3=0 and 2x−y+4=0 , and their respective lengths are √2 and 2√3. The equation of the hyperbola is
a) 25(x+2y−3)2−35(2x−y+4)2=1
b) 25(x−y−4)2−35(x+2y−3)2=1
c)25(2x−y+4)2−35(x+2y−3)2=1
d)2(x+2y−3)2−3(2x−y+4)2=101:51View SolutionThe locus of the foot of the perpendicular from the origin on each member of the family (4a+3)x−(a+1)y−(2a+1)=0 (a) (2x−1)2+4(y+1)2=5 (b) (2x−1)2+(y+1)2=5 (c) (2x+1)2+4(y−1)2=5 (d) (2x−1)2+4(y−1)2=5
01:52View SolutionFind the products:
(i) (2x+y)(2x−y)(4x2+y2)
(ii) (x−y5−1) (x+y5+1)02:58View SolutionFind matrices X and Y , if 2X+Y=[6−60−421] and X+2Y=[325−21−7] .
07:08View Solution

