The acute angle between two straight lines passing through the point M(−6,−8) and the points in which the line segment 2x+y+10=0 enclosed between the co-ordinate axes is divided in the ratio 1:2:2 in the direction from the point of its intersection with the x-axis to the point of intersection with the y-axis is: π3 (b) π4 (c) π6 (d) π12
π/3
π/4
π/6
π/12
The correct Answer is:B
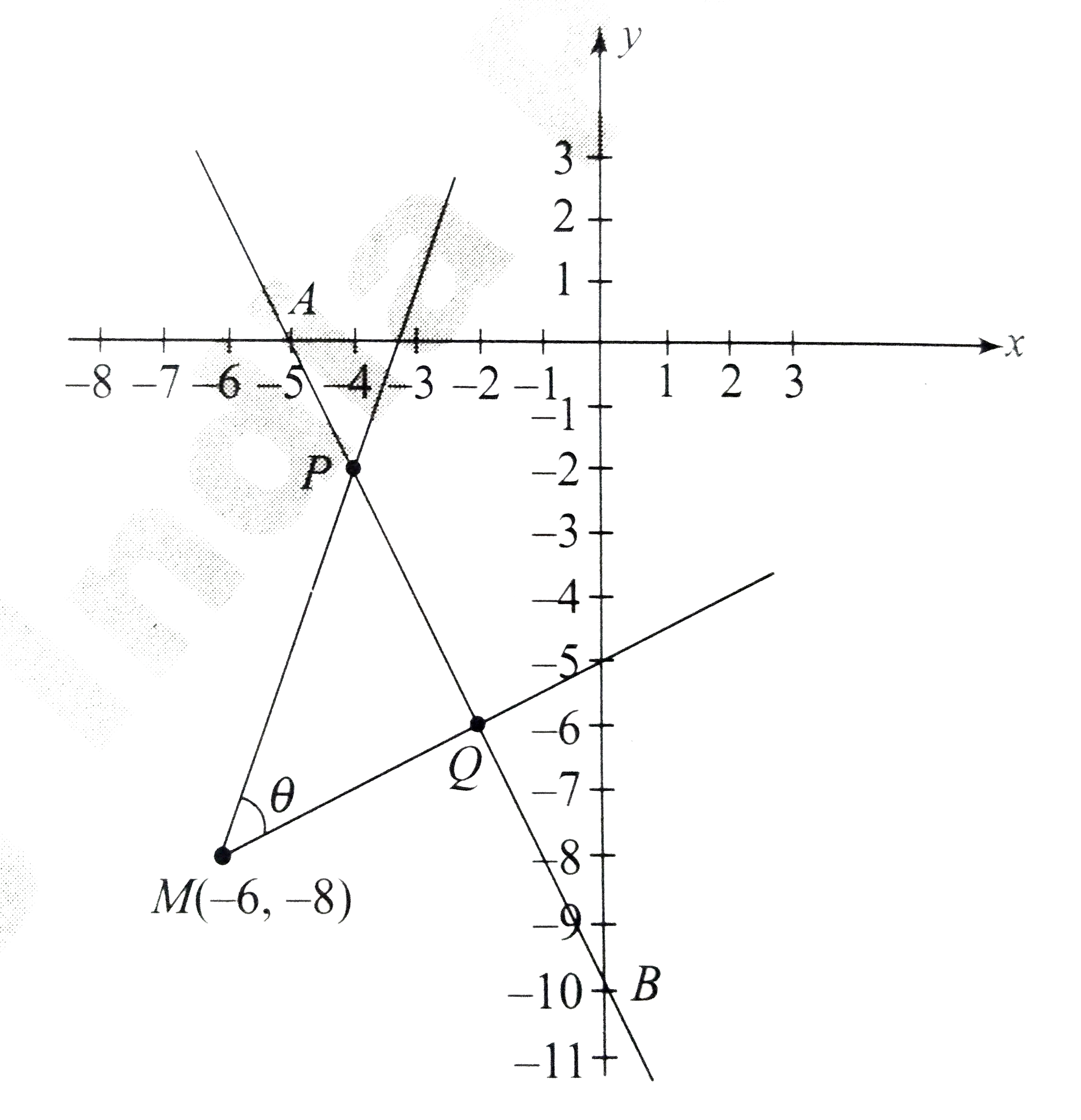
Le line 2x+y=10=0 intersect axis at A(−5,0) and B(0,−10) Lines through point M(−6,−8) intersect AB at P and Q,
Slope of AB is −2=tanα
Also AB=√25+100=5√5
Given AP:PQ:QB≡1:2:2
∴AP=√5 and AQ=3√5
Using parametric from of straight line AB, point P is (−5−√4cosα,0−√5sinα) or P(−4,−2)
Point Q is (−5−3√5cosα,0−3√5sinα) or Q(−2,−6)
∴ Let slopes of PM and QM be m1 and m2, respectively.
∴m1=3 and m2=12
Let θ be the acture angle between PM and QM.
∴tanθ=∣∣∣m1−m21+m2m2∣∣∣
⇒tanθ=1⇒θ=π4
Topper's Solved these Questions
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STRAIGHT LINEBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- STATISTICSBOOK - CENGAGE PUBLICATIONCHAPTER - STATISTICSEXERCISE - Archives
10 Videos
- STRAIGHT LINESBOOK - CENGAGE PUBLICATIONCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
Similar Questions
The angle between the tangents to the parabola y2=4ax at the points where it intersects with the line x−y−a=0 is (a)π3 (b) π4 (c) π (d) π2
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of point M.
View SolutionA straight line passes through the points A(-5, 2) and B(3,6). It intersects the co-ordinate axes at points C and D . M is a point on AB which divides CD in the ratio 1: 2. Find :
the co-ordinates of points C and D.
View SolutionIf the straight line ax+y+6=0 passes through the point of| intersection of the lines x+y+4=0and2x+3y+10=0,find α.
View SolutionIf the straight line passes through the point P(3,4) makes an angle π6 with x-axis and meets the line 12 x + 5 y + 10 = 0 at Q, Then the length of PQ is :
View SolutionIf the lines 2x+3y+1=0,6x+4y+1=0 intersect the co-ordinate axes in 4 points, then the circle passing through the points is
View SolutionA line passes through point(3,4) and the point of intersection of the lines 4x+3y=12and3x+4y=12 and length of intercepts on the co-ordinate axes are aandb, then ab is equal to
View SolutionThe angle between the tangents to the parabola y2=4ax at the points where it intersects with the line x−y−a=0 is π3 (b) π4 (c) π (d) π2
View SolutionIn what ratio is the line segment joining the points A(-4,2) and B(8,3) divided by the y-axis? Also, find the point of intersection.
View SolutionA straight line through the point A(1,1) meets the parallel lines 4x+2y=9 & 2x+y+6=0 at points P and Q respectively. Then the point A divides the segment PQ in the ratio:
View Solution
