If X is the foot of the directrix on the a parabola. PP' is a double ordinate of the curve and PX meets the curve again in Q. Then prove that PQ passes through the focus of the parabola.Solution in Bengali
line
circle
parabola
none of these
The correct Answer is:A
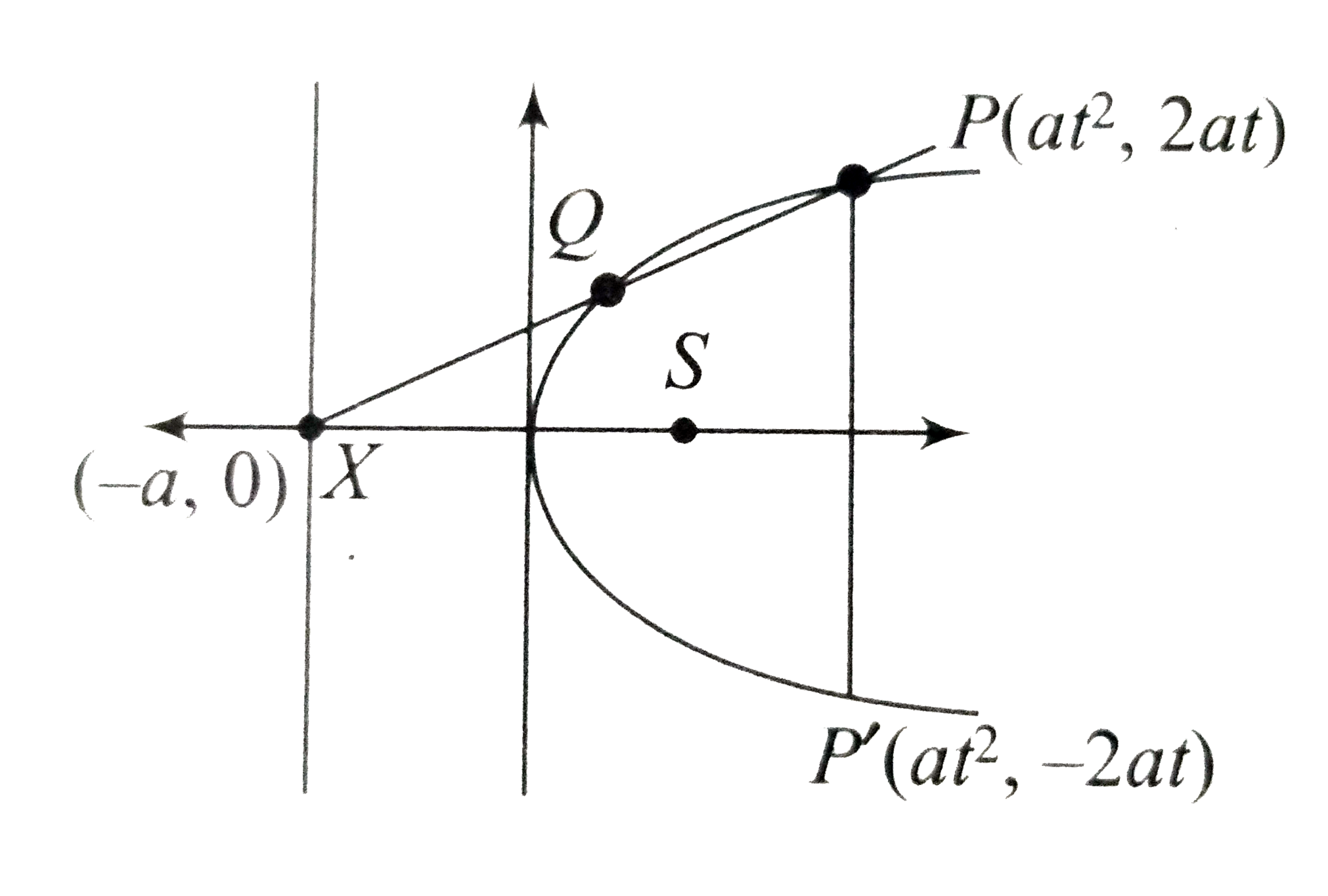
X:(−a,0)
PX:y=2at−0at2+a(x+a)
or (1+t2)y=2t(x+a)
Solving with parabola y2=4ax, we get
4t2(x+a)2(1+t2)2=4ax
or t2(x+a)2=ax(1+t2)2
or t2x2−(a+at4)x+at2=0
or xt2(x−at2)−a(x−at2)=0
or x=at2
∴Q:(at2,2at)
Thus P'(at2−2at) and Q(at2,2at), are extremities of focal chord.
So, tangents at P' and Q intersect on directrix.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Multiple Correct Answers Type10videos
PARABOLA
- BOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Matching Column Type1videos
PARABOLA
- BOOK - CENGAGE PUBLICATIONCHAPTER - PARABOLAEXERCISE - Comprehension Type2videos
PARABOLA
- BOOK - CENGAGE PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type5videos
PAIR OF STRAIGHT LINES
- BOOK - CENGAGE PUBLICATIONCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension8videos
PERMUTATION AND COMBINATION
Similar Questions
A family of curve S is given by S≡x2+2xy+y2−4x(1−λ)−4y(1+λ)+4, then S=0 represents (a) pair of straight line ∀λ∈R (b) straight line for exactly one value of λ (c) parabola ∀λ∈R−{0} (d) ellipse for three values of λ
07:18View SolutionAB is a chord of y2=4x such that normals at A and B intersect at C(9,6) and the tengent at A and B at point T, find (CT)2/13
08:33View SolutionIf cos−1.x2+cos−1.y3=π6, then prove that x24−xy2√3+y29=14
05:25View SolutionThe distance between the lines (x+7y)2+4√2(x+7y)−42=0 is_____________
View SolutionGiven are six 0's, five 1's and four 2's . Consider all possible permutations of all these numbers. [A permutations can have its leading digit 0].
How many permutations have the first 0 preceding the first 1 ?
(a) 15C4×10C5 (b) 15C5×10C4 (c) 15C6×10C5 (d) 15C5×10C5View SolutionPQ is a double ordinate of parabola y^(2)=4x which passes through the focus S.Delta POA is isosceles right angled triangle.Where A is on the axis of the parabola and PA meets the parabola at C and QA meets the parabola of B . Then
View SolutionLet S is the focus of the parabola y^(2)=4ax and X the foot of the directrix,PP' is a double ordinate of the curve and PX meets the curve again in Q. Prove that P'Q passes through focus.
08:18View SolutionIf X is the foot of the directrix on axis of the parabola. PP' is a double ordinate of the curve and PX meets the curve again in Q. Then prove that P' Q passes through fixed point which is
06:59View SolutionPQ is the double ordinate of the parabola y2=4x which passes through the focus S. ΔPQA is an isosceles right angle triangle, where A is on the axis of the parabola to the right of focus. Line PA meets the parabola at C and QA meets the parabola at B.
The of trapezium PBCQ isView SolutionPQ is the double ordinate of the parabola y2=4x which passes through the focus S. ΔPQA is an isosceles right angle triangle, where A is on the axis of the parabola to the right of focus. Line PA meets the parabola at C and QA meets the parabola at B.
The circumradius of trapezium PBCQ is05:44View SolutionPQ is the double ordinate of the parabola y2=4x which passes through the focus S. ΔPQA is an isosceles right angle triangle, where A is on the axis of the parabola to the right of focus. Line PA meets the parabola at C and QA meets the parabola at B. The ratio of the inradius of ΔABC and that of ΔPAQ is
01:47View SolutionIf normals at the ends of the double ordinate x = 4 of parabola y2=4x meet the curve again in P and P' respectively, then PP' =
12:41View SolutionLet S is the focus of the parabola y2=4ax and X the foot of the directrix, PP’ is a double ordinate of the curve and PX meets the curve again in Q. Prove that P’Q passes through focus.
07:46View SolutionThe normal at a point P on the parabola y2=4ax cuts the curve again at Q . If M is the midpoint of PQ then the product of the ordinates of P and M is
15:05View SolutionLet S is the focus of the parabola y2=4ax and X the foot of the directrix, PP' is a double ordinate of the curve and PX meets the curve again in Q. Prove that P'Q passes through focus.
09:31View SolutionIn the parabola y2=4x, the ends of the double ordinate through the focus are P and Q. Let O be the vertex. Then the length of the double ordinate PQ is
07:10View Solution

